Если необходимо знать интенсивность излучения, рассеянного пространственным распределением электронов внутри каждой элементарной ячейки, то необходим более подробный анализ. Наиболее простой метод предложен Лауэ, который состоит в суммировании вкладов от элементарных волн, рассеянных от каждого элемента кристалла.
Найдем направления распространения волн, выходящих из кристалла, относительно заданного направления распространения падающей волны и рассчитаем интенсивность дифракции электромагнитного излучения (фотонов) на кристаллической решетке, имеющей примитивную элементарную ячейку в виде косоугольного параллелепипеда с векторами 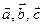 . Пусть вдоль векторов
. Пусть вдоль векторов 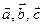 решетка имеет соответственно по N, M, P узлов (см. рис. 2.2).
решетка имеет соответственно по N, M, P узлов (см. рис. 2.2).
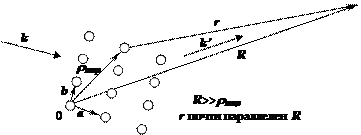 |
| Рис. 2.2. Рассеяние электромагнитных волн узлами кристаллической решетки. |
Пусть на такую решетку падает волна с волновым вектором 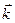 , и частотой
, и частотой 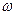 , а отраженная волна имеет волновой вектор
, а отраженная волна имеет волновой вектор 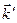 и частоту
и частоту 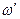 . Рассмотрим случай, когда не происходит изменения частоты у рассеянного излучения:
. Рассмотрим случай, когда не происходит изменения частоты у рассеянного излучения: 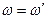 , а значит (так как
, а значит (так как 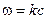 ) и
) и 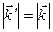 .
.
Выразим направление отраженной волны через волновой вектор падающей волны 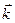 и векторы примитивных трансляций
и векторы примитивных трансляций 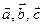 кристаллической решетки.
кристаллической решетки.
Вектор напряженности электрического поля 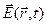 в падающей волне в точке
в падающей волне в точке 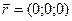 пусть задается как
пусть задается как
Вектор напряженности электрического поля 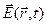 в падающей волне в точке
в падающей волне в точке 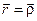 пусть задается как
пусть задается как
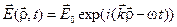
Вектор напряженности электрического поля 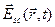 в рассеянной волне в точке
в рассеянной волне в точке 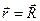 :
:
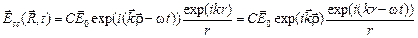 (25)
(25)
С - коэффициент пропорциональности
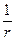 - для сохранения энергии в потоке рассеянной волны.
- для сохранения энергии в потоке рассеянной волны.
Эта волна взаимодействует с рассеивающим центром, находящимся в точке ρ, в результате чего образуется рассеянная волна, выражение для которой можно записать в виде:
Наша задача заключается в суммировании элементарных волн, рассеянных всеми центрами рассеяния в кристалле, в результате чего мы получим амплитуду суммарной рассеянной волны в точке с радиус-вектором R, проведенным из начала координат О внутри кристалла. В этой точке расположен счетчик фотонов. Из рис.2.15 мы видим, что расстояние между рассеивающим центром и точкой наблюдения равно.
Для вектора 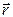 можно записать (см. рис.2.2.):
можно записать (см. рис.2.2.):
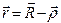
Возведя обе части выражения в квадрат, получим:
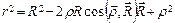
Если извлечь квадратный корень и пренебречь членами порядка 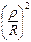 и выше, то получим:
и выше, то получим: 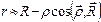 .
.
Тогда полный пространственный фазовый множитель рассеянной волны в выражении (25) можно представить в виде:
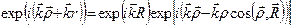
Так как 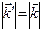 , а направление вектора рассеянной волны
, а направление вектора рассеянной волны 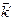 совпадает с направлением
совпадает с направлением 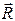 , то
, то
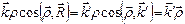
Следовательно, фазовый множитель можно записать так:
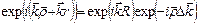
где 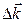 - изменение волнового вектора в результате рассеяния:
- изменение волнового вектора в результате рассеяния: 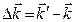
с учетом вышеизложенного волну, рассеянную центром рассеяния в точке 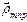 , можно представить как:
, можно представить как:
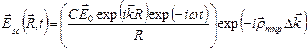
Выражение для суммарного рассеяния в данном направлении от решетки точеных атомов можно получить с помощью суммирования выражения (33) для 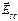 по всем точкам решетки. В этом случае сумма фазовых множителей определяется как:
по всем точкам решетки. В этом случае сумма фазовых множителей определяется как:
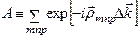
Кристалл имеет форму параллелепипеда и каждый узел решетки рассеивает падающую волну. Центры рассеяния расположены в каждом узле этой решетки: 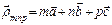 , где m,n,p – целые числа. Тогда величина суммарного рассеянного излучения пропорциональна
, где m,n,p – целые числа. Тогда величина суммарного рассеянного излучения пропорциональна
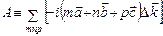
Величину А называют амплитудой рассеяния.
Сумма, взятая по узлам решетки, максимальна, когда 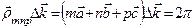 (*)
(*)
для всех узлов решетки, так как каждый член, имеющий форму 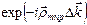 , равен единице.
, равен единице.
Величина 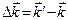 удовлетворяет условию дифракции (*), если одновременно выполняются соотношения для целых чисел h,k,l:
удовлетворяет условию дифракции (*), если одновременно выполняются соотношения для целых чисел h,k,l:
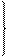
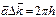
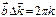 уравнение дифракции Лауэ
уравнение дифракции Лауэ
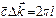
Рассмотрим вектор 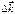 , равный
, равный 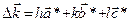 (),
(),
где h,k,l – целые числа, входящие в уравнение Лауэ ().
Подставляя 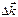 из (), видно, что () есть решение уравнений (), если
из (), видно, что () есть решение уравнений (), если
1. 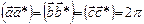
2. 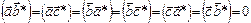
Следовательно, 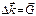 , где
, где 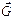 - вектор обратной решетки (смотри лекцию №1).
- вектор обратной решетки (смотри лекцию №1).
Таким образом, условие дифракции: 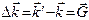
Возведем обе части этого соотношения в квадрат и получим:
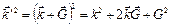
Так как 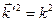 , то
, то 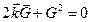 (**)
(**)
Соотношение (**) эквивалентно закону Брэгга-Вульфа.
2.3. Геометрическая интерпретация уравнения Лауэ. Построение Эвальда.
Пространство обратной решетки называется пространство Фурье. В Фурье пространстве правило отбора 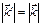 и
и 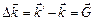 имеют геометрическую интерпретацию – построение Эвальда (рис. 2.3).
имеют геометрическую интерпретацию – построение Эвальда (рис. 2.3).
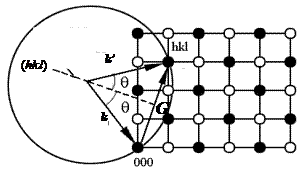 | ||
| Рис. 2.3. Построение Эвальда. |
Построение Эвальда заключается в следующем:
1. Найдем обратную решетку кристалла, подсчитав длины  . Построим сетку обратной решетки. Выберем узел обратной решетки за начальный. Направление вектора
. Построим сетку обратной решетки. Выберем узел обратной решетки за начальный. Направление вектора 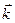 совпадает с направлением падающей волны. Вектор
совпадает с направлением падающей волны. Вектор 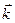 заканчивается на произвольном узле обратной решетки. Обозначим этот узел 0 0 0.
заканчивается на произвольном узле обратной решетки. Обозначим этот узел 0 0 0.
2. Рисуем сферу радиусом 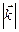 = 2p/l с центром в начале вектора
= 2p/l с центром в начале вектора 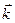 . Если сфера пересекает еще один узел обратной решетки – наблюдается дифракция. Дифрагированная волна распространяется вдоль
. Если сфера пересекает еще один узел обратной решетки – наблюдается дифракция. Дифрагированная волна распространяется вдоль 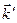 .
. 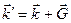
Построением Эвальда очень удобно пользоваться для предсказания углов поворота кристалла и направления дифрагированных лучей. Обратная решетка жестко связана с кристаллической решеткой кристалла, при повороте кристалла вместе с ним поворачивается и обратная решетка. Для наблюдения дифракции кристалл поворачивают так, чтобы вектор рассеяния совпал бы с одним из узлов обратной решетки. С помощью геометрии можно вычислить необходимые углы поворота обратной решетки (и кристалла), а затем определить, под какими углами должен быть расположен детектор излучения, регистрирующий волны с вектором 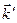 .
.
Из рис. 2.3 видно, что между длинами векторов 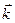 и
и 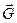 существует связь:
существует связь:
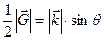 Þ
Þ 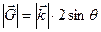 .
.
Так как 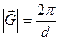 (смотри лекцию №1) и
(смотри лекцию №1) и 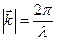 , то
, то
получаем формулу Брэгга-Вульфа: 2 d sinq= n l (в данном случае n =1).
 2015-04-01
2015-04-01 2682
2682








