Корреляционный анализ

Существенным моментом в статистических исследованиях является выявление зависимости между переменными, характеризующими различные свойства объектов.

Между случайными величинам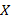и и 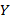может существовать:

1. Функциональная взаимосвязь - зависимость, при которой каждому значению переменно 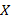соответствует точно определенной значение .

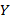2. Стохастическая взаимосвязь - связь, при которой изменение значения одной переменной приводит к изменению закона распределения.

3. Статистическая взаимосвязь - зависимость, при которой значение одной переменной изменяется в среднем от того, какие значения принимает другая переменная.

Задачей корреляционного анализа является доказательство наличия этой связи и ее силы. Выявление характера (в аналитической форме) этой связи относится к классу задач регрессионного анализа.

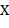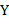Если совместное распределение и является нормальным, то статистические выводы основывают на выборочном коэффициенте линейной корреляции, в остальных случаях используют коэффициенты ранговой корреляции Кендалла и Спирмена, а для качественных признаков – критерий хи-квадрат.

Независимо от типа, две или более переменных связаны (зависимы) между собой, если наблюдаемые значения этих переменных распределены согласованным образом. Другими словами, мы говорим, что переменные зависимы, если их значения систематическим образом согласованы друг с другом в имеющихся у нас наблюдениях.

Рассмотрим способы измерения связи между двумя случайными переменными. Пусть исходными данными является набор случайных векторов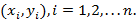

Выборочной ковариацией, или корреляционным моментом, называется величина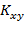

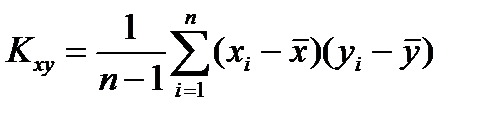, (6.5)

где 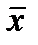, 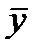– средние значения величин.

Ковариация описывает как степень разброса возможных значений случайных величин 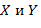относительно своих средних значений, так и статистическую связь между ними. Для описания собственно степени статистической связи между случайными величинами используют безразмерную величину, называемую парным коэффициентом корреляции.

Выборочным линейным парным коэффициентом корреляции Пирсона называется величина :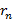

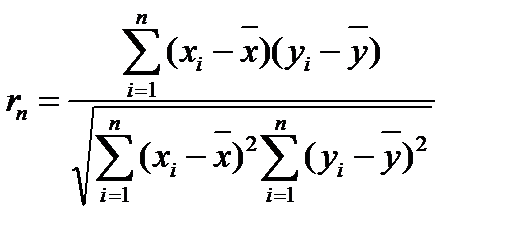(6.6)

Коэффициент корреляции Пирсона 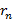имеет четкий смысл как характеристика степени тесноты связи только для нормально распределенных величин. Значение
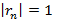свидетельствует о наличии полной функциональной зависимости между этими величинами, в то время как значение 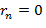говорит об их полной независимости.

Коэффициент корреляции Пирсона 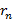, средние и дисперсии нормально распределенных случайных величин 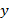и 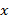дают исчерпывающие сведения об их стохастической зависимости, так как однозначно определяют их двумерный закон распределения.

Статистическую связь между переменным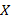и и 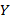можно наглядно продемонстрировать с помощью диаграмм рассеяния. Точки данных на диаграмме изображаются точками в двумерном пространстве, где оси соответствуют переменным. Две координаты ( 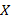и 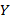), которые определяют положение каждой точки, соответствуют значениям двух переменных для этой точки. Если две переменные сильно связаны, то множество точек данных принимает определенную форму (например, прямой линии или кривой). Если же переменные не связаны, то точки образуют «облако». На рис. 6.5 представлены примеры диаграмм рассеяния для различных значений коэффициента корреляции.

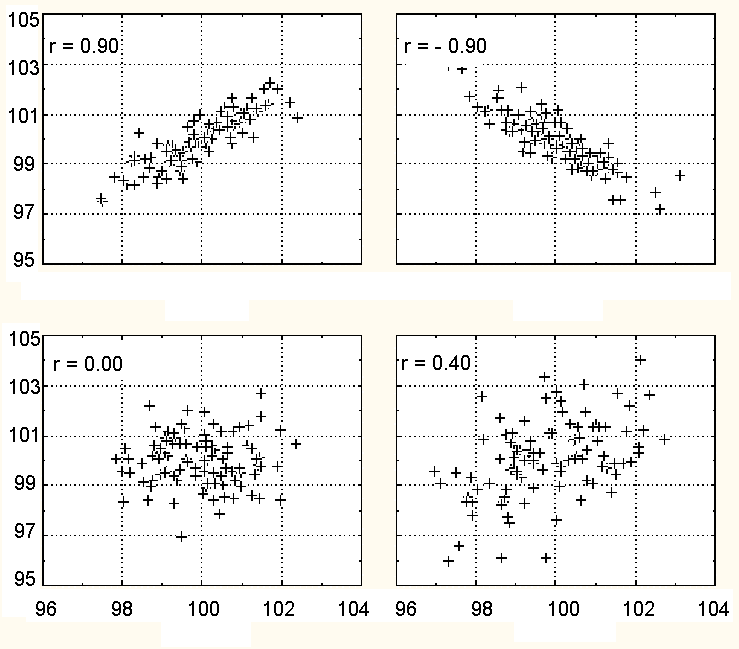
Рис. 6.5. Примеры диаграмм рассеяния для различных значений коэффициента корреляции

Предположим, что необходимо выполнить исследование зависимости между среднемесячными доходами X на семью (в тыс. руб.) и расходами Y на покупку кондитерских изделий (в руб.). Целями исследования зависимости между переменными являются доказательство наличия связи между ним и изучение этой связи. Для доказательства наличия связи между двумя случайными величинами и применяют корреляционный анализ. На основе данных наблюдений построена матрица корреляции и диаграмма размещения (рис.6.6) с использованием возможностей аналитической платформы Deductor.

Анализ рис. 6.6 позволяет сделать вывод о наличии сильной линейной статистической связи между среднемесячными доходами семьи и затратами на приобретение ею кондитерских изделий. При этом связь имеет положительную тенденцию, т.е. с ростом переменной 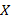наблюдается увеличение отклика .

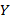Коэффициент корреляции Пирсона представляет собой меру линейной зависимости двух переменных. Если возвести его в квадрат, то полученное значение коэффициента детерминации 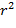представляет долю вариации, общую для двух переменных (иными словами, степень зависимости или связанности двух переменных). Чтобы оценить зависимость между переменными, нужно знать как «величину» корреляции, так и ее значимость.

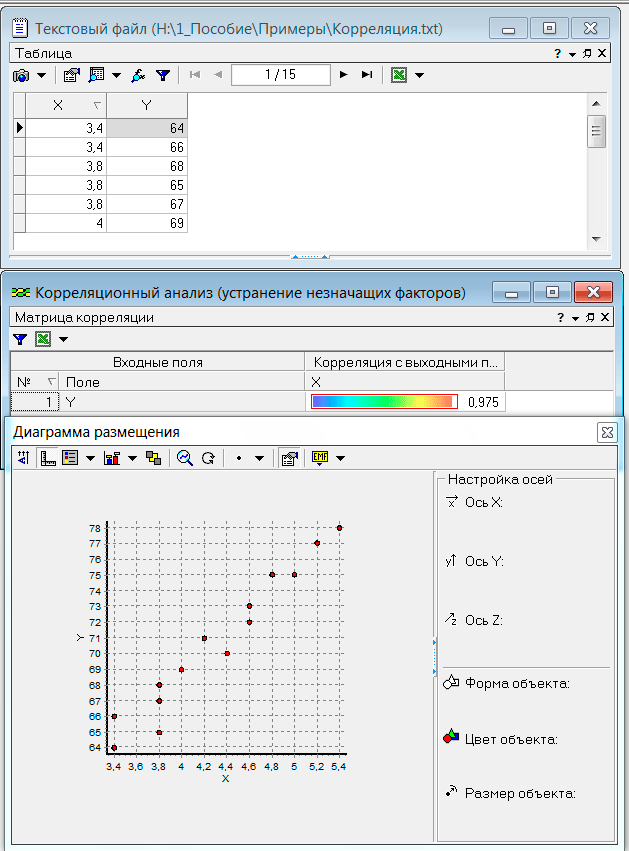
Рис. 6.6. Результаты корреляционного анализа данных

Уровень значимости, вычисленный для каждой корреляции, представляет собой главный источник информации о надежности корреляции. Критерий значимости основывается на предположении, что распределение остатков (т.е. отклонений наблюдений от регрессионной прямой) для зависимой переменной является нормальным (с постоянной дисперсией для всех значений независимой переменной ). Исследования методом Монте-Карло показали, что нарушение этих условий не является абсолютно критичным, если размеры выборки не слишком малы, а отклонения от нормальности не очень большие.

Следует подчеркнуть, что при изучении зависимостей очень важным является построение и изучение диаграмм рассеяния. Основные проблемы могут быть связаны с выбросами (рис. 6.7), неоднородностью данных, нелинейной зависимостью. Обычно считается, что выбросы представляют собой случайную ошибку, которую следует контролировать. Очевидно, что выбросы могут не только искусственно увеличить значение коэффициента корреляции, но и уменьшить существующую корреляцию. В статистических исследованиях применяют различные численные методы удаления выбросов. Например, исключаются все значения, которые выходят за границы ±2 стандартных отклонений вокруг выборочного среднего.

Отсутствие однородности в выборке также является фактором, смещающим (в ту или иную сторону) выборочную корреляцию. Коэффициент корреляции может быть вычислен по данным, которые поступили из двух или нескольких групп, различающихся по коррелированности признаков. Таким образом, данные каждой группы сильно различаются на диаграмме рассеяния (рис. 6.8). В данном примере высокая корреляция вовсе не отражает «истинную» зависимость между двумя переменными, которая практически отсутствует (рис. 6.8 и рис. 6.9). Если разбиение данных на группы не очевидно, применяются многомерные методы разведочного анализа, например, кластерный анализ.

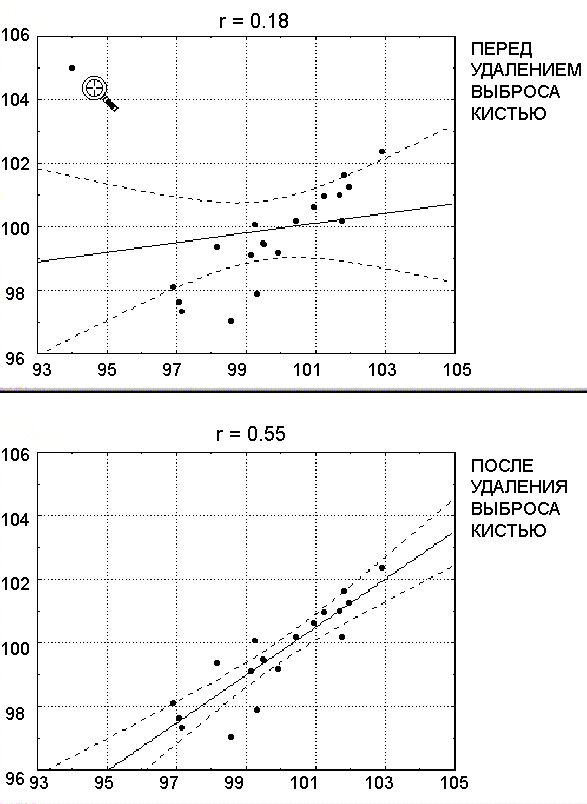
Рис. 6.7. Влияние выброса на значение коэффициента корреляции [9]

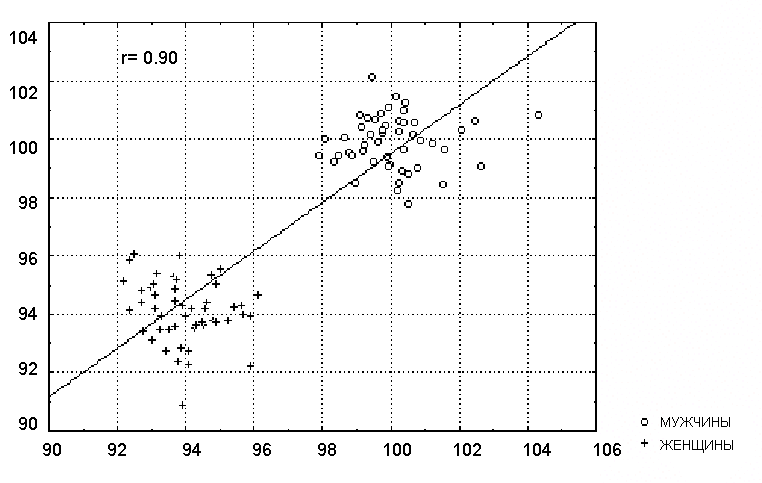
Рис. 6.8. Диаграмма рассеяния для неоднородных групп

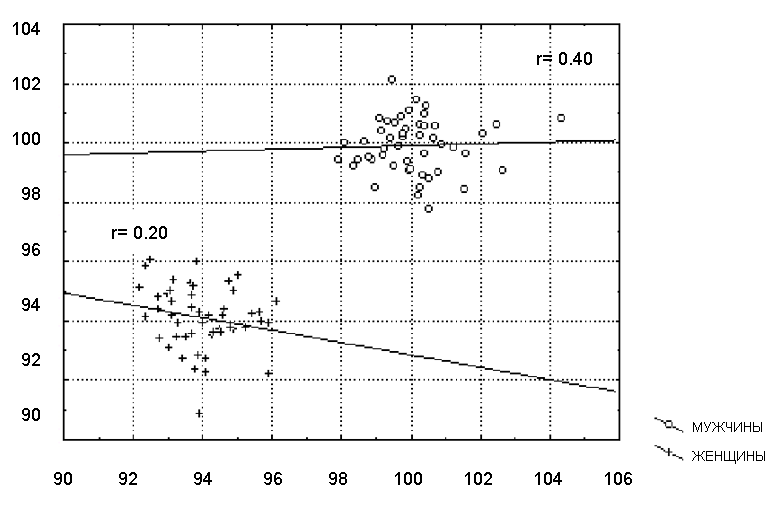
Рис. 6.9. Коэффициенты корреляции, полученные для каждой группы в отдельности [10]

Коэффициент корреляция Пирсона 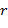хорошо подходит для описания линейной зависимости. Использование r как меры зависимости между произвольным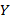и и 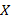может привести к ошибочным выводам, так как 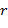может равняться нулю даже тогда, когда 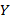строго зависит от .

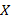Для количественных переменных, не подчиняющихся нормальному распределению, а также для переменных, принадлежащих к порядковой шкале, вместо коэффициента Пирсона используются непараметрические коэффициенты корреляции. К ним относятся коэффициент ранговой корреляции Спирм е на, коэффициент ранговой корреляции 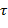Кендалла и др.

Ранговые коэффициенты определяются не непосредственно через значения переменных, а через их ранги. Для этого отдельным значениям переменных присваиваются ранговые места, которые впоследствии обрабатываются с помощью соответствующих формул.

Для расчета непараметрического коэффициента ранговой корреляции Спирмена необходимо предварительно рассчитать ранги для всех значений вариационных рядов 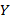и 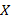, то есть для каждого 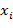рассчитать его ранг 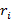в вариационном ряду, построенном по выборке, для каждого 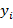рассчитать его ранг 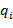в вариационном ряду, построенном по выборке. Затем для набора из 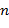(i = 1,..., n) пар рангов вычисляется линейный коэффициент корреляции.

Коэффициент ранговой корреляции Спирмена рассчитывается по формуле:

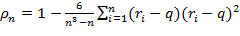(6.7)

Для совпадающих ранжировок 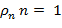, а для противоположных он равен -1. Во всех остальных случаях .

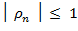Следует подчеркнуть, что коэффициент ранговой корреляции Спирмена остается постоянным при любом строго возрастающем преобразовании шкалы измерения результатов наблюдений. Другими словами, он является адекватным в порядковой шкале, как и другие ранговые статистики.

В качестве примера выявим взаимосвязь между уровнем развития предпринимательства и уровнем государственной поддержки в регионах России. Уровень развития предпринимательства будем оценивать по интегральному индексу развития малого и среднего предпринимательства, учитывающему следующие показатели оценки:

· количество субъектов малого и среднего предпринимательства в расчете на 100 тыс. жителей региона;

· доля среднесписочной численности занятых на малых и средних предприятиях в общей среднесписочной численности занятых в регионе;

· выручка от реализации товаров (работ, услуг) малых и средних предприятий в расчете на 1 занятого на малых и средних предприятиях;

· объем инвестиций в основной капитал малых и средних предприятий в расчете на 1 занятого на малых и средних предприятиях.

При расчете индекса учитывались результаты деятельности как малых (включая микро) и средних предприятий, так и индивидуальных предпринимателей. Результаты проведенной оценки и их ранжирование представлены в таблице 6.1.

Проведенные расчеты показывают фактическое отсутствие статистически значимой связи между объемами оказываемой государством поддержки и результатами деятельности субъектов малого и среднего предпринимательства в регионах. Так, согласованность рангов по двум индексам оказалась крайне низкой (значение коэффициента корреляции рангов Спирмена составило 0,123), что указывает на то, что в рамках модельных упрощений объемы оказанной государственной поддержки не значительно влияют на место региона по уровню развития малого и среднего предпринимательства среди других регионов.