Результаты проведения опытов и испытаний могут зависеть от некоторых факторов, влияющих на изменчивость средних значений случайной величины 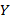 . Значения факторов называют уровнями факторов, а величину
. Значения факторов называют уровнями факторов, а величину 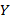 называют результативным признаком. Например, объем выполненных на стройке работ может зависеть от работающей бригады. В этом случае номер бригады является уровнем фактора, а объем работ за смену – результативным признаком.
называют результативным признаком. Например, объем выполненных на стройке работ может зависеть от работающей бригады. В этом случае номер бригады является уровнем фактора, а объем работ за смену – результативным признаком.
Метод дисперсионного анализа, или ANOVA (Analysis of Variance – дисперсионный анализ), служит для исследования статистической значимости различия между средними при трех и более выборках (уровнях фактора). Для сравнения средних в двух выборках используется t -критерий.
Процедура сравнения средних называется дисперсионным анализом, так как при исследовании статистической значимости различия между средними нескольких групп наблюдений проводится анализ выборочных дисперсий. Фундаментальная концепция дисперсионного анализа была предложена Фишером.
Сущность метода состоит в разделении общей дисперсии на две части, одна из которых обусловлена случайной ошибкой (то есть внутригрупповой изменчивостью), а вторая связана с различием средних значений. Последняя компонента дисперсии затем используется для анализа статистической значимости различия между средними значениями. Если это различие значимо, нулевая гипотеза отвергается и принимается альтернативная гипотеза о существовании различия между средними.
Переменные, значения которых определяется с помощью измерений в ходе эксперимента (например, экономическая эффективность, урожайность, результат тестирования), называются зависимыми переменными или признаками. Переменные, которыми можно управлять при проведении эксперимента (например, уровень управления, тип почвы, методы обучения) называются факторами или независимыми переменными.
В классическом дисперсионном анализе полагается, что исследуемые величины имеют нормальное распределение с постоянной дисперсией и средними значениями, которые могут отличаться для разных выборочных совокупностей. В качестве критерия проверки нулевых гипотез используется отношение дисперсии групповых средних и остаточной дисперсии. Однако было показано, что дисперсионный анализ справедлив и для негауссовских случайных величин, причем при объеме выборок для каждого уровня фактора n > 4 погрешность невысока. Если требуется высокая точность выводов, а распределение неизвестно, то следует использовать непараметрические критерии, например, использовать ранговый дисперсионный анализ.
Однофакторный дисперсионный анализ
Пусть проводится m групп измерений значений случайной величины Y при различных уровнях значения некоторого фактора, и a1, a2, am – математическое ожидание результативного признака при уровнях фактора A (1), A (2), A (m) (i =1, 2, m) соответственно.
Предположение о независимости результативного признака от фактора сводится к проверке нулевой гипотезы о равенстве групповых математических ожиданий
H0: a1 = a2 = am (6.12)
Проверка гипотезы возможна при соблюдении следующих требований для каждого уровня фактора:
1) наблюдения независимы и проводятся в одинаковых условиях;
2) измеряемая случайная величина имеет нормальный закон распределения с постоянной для различных уровней фактора генеральной дисперсией σ 2. То есть справедлива гипотеза
H0: σ12 = σ22 = σ m 2.
Для проверки гипотезы о равенстве дисперсий трех и более нормальных распределений применяется критерий Бартлета.
Если гипотеза H0: σ12 = σ22 = σ m 2 подтверждается, то приступают к проверке гипотезы о равенстве групповых математических ожиданий H0: a1 = a2 = am, то есть собственно к дисперсионному анализу. В основе дисперсионного анализа лежит положение, что изменчивость результативного признака вызвана как изменением уровней фактора А, так и изменчивостью значений случайных неконтролируемых факторов. Случайные факторы называются остаточными.
Можно доказать, что общая выборочная дисперсия может быть представлена в виде суммы дисперсии групповых средних и средней из групповых дисперсий
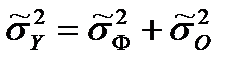 , где
, где
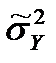 – общая дисперсия выборки;
– общая дисперсия выборки;
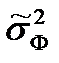 – дисперсия групповых средних (
– дисперсия групповых средних (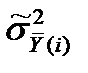 ), рассчитанных для каждого уровня фактора;
), рассчитанных для каждого уровня фактора;
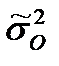 – средняя по групповым дисперсиям (
– средняя по групповым дисперсиям (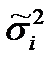 ), рассчитанным для каждого уровня фактора.
), рассчитанным для каждого уровня фактора. 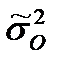 связана с влиянием на Y остаточных (случайных) факторов.
связана с влиянием на Y остаточных (случайных) факторов.
Перейдя от разложения для генеральной дисперсии к выборочным значениям, получим
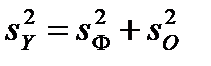 , (6.13)
, (6.13)
где
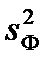 представляет собой взвешенную сумму квадратов отклонений выборочных средних по каждому уровню A(i) от общего выборочного среднего,
представляет собой взвешенную сумму квадратов отклонений выборочных средних по каждому уровню A(i) от общего выборочного среднего,
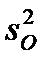 - среднее значение квадратов отклонений внутри уровней.
- среднее значение квадратов отклонений внутри уровней.
Случайные величины 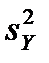 ,
, 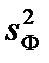 ,
, 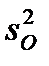 имеют следующие значения для степеней свобод соответственно: n - 1, m - 1, n - m. Здесь n – общее число выборочных значений, m – число уровней фактора.
имеют следующие значения для степеней свобод соответственно: n - 1, m - 1, n - m. Здесь n – общее число выборочных значений, m – число уровней фактора.
В математической статистике доказывается, что если нулевая гипотеза о равенстве средних (10.8) верна, то величина
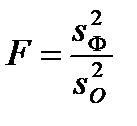
имеет F -распределение с числом степеней свободы k = m - 1 и l = n- m, то есть
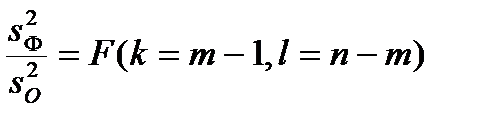 (6.14)
(6.14)
При выполнении нулевой гипотезы внутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. В дисперсионном анализе, как правило, числитель в больше знаменателя. В противном случае считается, что наблюдения не подтверждают влияние фактора на результирующий признак и дальнейший анализ не проводится. Полученные внутригрупповые дисперсии можно сравнить с помощью F -критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1.
В связи с этим для проверки гипотезы (6.12) с помощью F -критерия анализируется правосторонняя критическая область 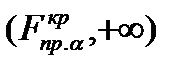 .
.
Если рассчитанное значение F попадает в указанный интервал, то нулевая гипотеза отвергается, и считается установленным влияние фактора А на результативный признак Y.
Приведем пример расчета сумм квадратов и выборочных дисперсий. Рассмотрим набор данных, представленный в таблице 6.2. В данном примере требуется определить, есть ли значимое различие в производительности бригад.
Таблица 6.2. Пример расчета сумм квадратов
| Объем выполненной работы | ||||
| Номер смены | Бригада 1 | Бригада 2 | Бригада 3 | Бригада 4 |
| Число наблюдений | ||||
| Средние по группам | 142,75 | 150,25 | 147,5 | 152,75 |
| Общее среднее | 148,31 |
 2015-04-01
2015-04-01 7632
7632
