Регрессионный анализ

Регрессионный анализ является одним из самых распространённых методов обработки результатов наблюдений и в ряде случаев выступает основой для таких методов как планирование эксперимента, многомерный статистический анализ, дисперсионный анализ и др.

В регрессионном анализе различают результирующую (зависимую) переменную 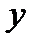и объясняющие (предикторные) переменные 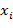. Функция 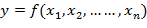называется функцией регрессии и показывает, каким будет в среднем значение переменной 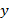, если переменные 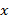примут конкретные значения. Уравнения регрессионной связи могут быть представлены в следующем виде:

y(X) = f(X) + ε(X),

Eε(X) ≡ 0, где (6.8)

ε (X) – случайная остаточная составляющая (регрессионные остатки),

Eε (X) – ее математическое ожидание.

Наличие остаточной составляющей связано, во-первых, с существованием факторов, не учтенных в объясняющих переменных, и, во-вторых, со случайной погрешностью в измерении результирующего фактора.

Стандартный подход основан на предположении, функция регрессии описывается линейной зависимостью вида:

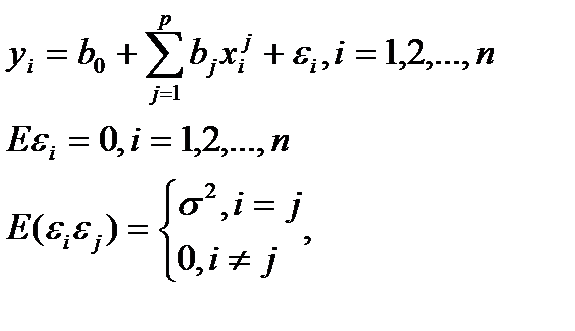(6.9)

где p – число объясняющих переменных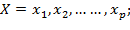

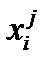– значение i -й компоненты j -й объясняющей переменной;

n – число измерений результирующей переменной y =(y₁, y₂,..., y_n);

ε =(ε₁, ε₂,..., ε_n) – случайная компонента;

b =(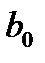, ,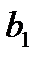..., 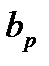) – неизвестные параметры регрессии.

Ранг матрицы X = p+1 < n.

Таким образом, в рамках классической линейной модели множественной регрессии рассматриваются только линейные функции регрессии, где объясняющие переменные играют роль неслучайных параметров. Кроме того предполагается, что случайные регрессионные остатки взаимно некоррелированны и имеют постоянную дисперсию σ². Независимость дисперсий остатков от значений объясняющих переменных называется гомоскедастичностью регрессионных остатков.

Следующим требованием является максимальность ранга матрицы 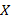, что означает, что не должно существовать строгой линейной зависимости между объясняющими переменными.

Таблица 6.1 - Рейтинг регионов по уровню развития малого и среднего предпринимательства [11]

Российская Федерация (справочно)	Интегральный индекс	Рейтинг господдержки	Российская Федерация (справочно)	Интегральный индекс	Рейтинг господдержки
Алтайский край			Республика Хакасия
Амурская область			Рязанская область
Архангельская область			Самарская область
Астраханская область			Саратовская область
Волгоградская область			Свердловская область
Вологодская область			Ставропольский край
г. Санкт-Петербург			Тверская область
Еврейская автономная область			Ульяновская область
Забайкальский край			Ханты-Мансийский АО
Ивановская область			Чеченская Республика
Иркутская область			Чувашская Республика
Кабардино-Балкарская Республика			Ярославская область
Калининградская область			Республика Адыгея
Калужская область			Республика Башкортостан
Карачаево-Черкесская Республика			Республика Бурятия
Кировская область			Республика Дагестан
Краснодарский край			Республика Ингушетия
Красноярский край			Республика Карелия
Курганская область			Республика Коми
Ленинградская область			Республика Марий Эл
Липецкая область			Республика Мордовия
Магаданская область			Республика Саха (Якутия)
Московская область			Республика Северная Осетия - Алания
Ненецкий АО			Республика Татарстан
Нижегородская область			Орловская область
Новгородская область			Пермский край
Оренбургская область			Псковская область

Для решения уравнений регрессии в общем случае используется метод наименьших квадратов (МНК), позволяющий подобрать такие оценки параметров функции регрессии 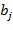, при которых регрессионные значения результирующего показателя как можно меньше отличались от наблюденных значений 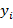. В тех случаях, когда вводится дополнительное предположение о нормальном распределении регрессионных остатков, используется метод максимального правдоподобия.

После того, как получены коэффициенты регрессионной зависимости, следует определить величину степени стохастической взаимосвязи результирующей переменной 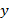и факторов 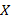. Она определяется через общую дисперсию показателя, факторную и остаточную дисперсии.

Вариация результирующей переменной 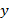обусловлена варьированием значений объясняющей переменной 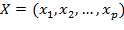и поведением случайных остатков 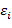_i. Общая дисперсия результирующей переменной 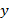равна

,

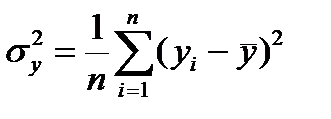где 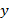⎼ среднее значение переменной .

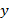Факторная дисперсия 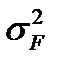результирующей переменной 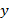отражает только влияние основных факторов:

,

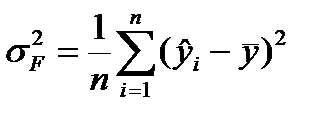где 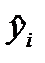- теоретические значения результирующего показателя, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии.

Остаточная дисперсия 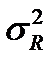результирующего показателя y отражает влияние только остаточных факторов:

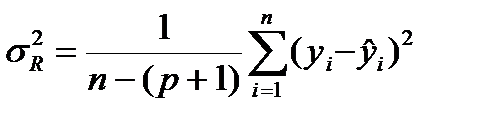
При наличии корреляционной связи результирующей переменной и факторов выполняется соотношение

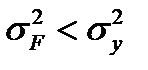, причем .

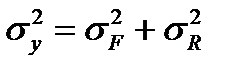Для анализа общего качества уравнения линейной многофакторной регрессии используется коэффициент детерминации R², рассчитываемый по формуле

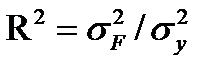
Он определяет долю вариативности результирующего показателя, обусловленную изменением факторных признаков.

Многие важные зависимости в экономике являются нелинейными. В качестве примера таких регрессионных моделей можно привести зависимость между объемом произведенной продукции и основными факторами производства, функции спроса.

Если предварительный анализ показывает, что искомая зависимость нелинейна, то выполняются следующие шаги.

Производится попытка так преобразовать анализируемые переменные y, x₁, x₂,..., x_p, чтобы искомая зависимость была представлена в виде линейного соотношения между преобразованными переменными. Такой процесс называют процедурой линеаризации модели, а сами модели называются внутренне линейными [30].

Например, если рассматривается экспоненциальная модель вида

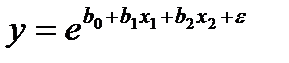, (6.10)

то после логарифмирования получим модель, имеющую форму линейной регрессии:

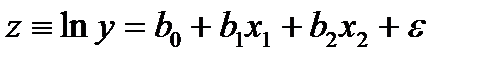(6.11)

Аналогичные свойства имеют зависимости гиперболического типа и логарифмического типа.

Если же линеаризующее преобразование подобрать не удается, то есть модель внутренне нелинейна, то в этом случае требуется привлечение соответствующих методов нелинейной оптимизации [31].