В основе дескриптивного (описательного) анализа лежат такие статистические показатели как средняя величина, мода, медиана, стандартное отклонение и другие. Они представляют собой характеристики переменных - величин, которые в исследованиях можно измерять, контролировать или варьировать. Применение описательных статистик позволяет рассматривать не все значения переменной, а сформировать общее представление о значениях, которые принимает переменная. Подробная информация о свойствах описательных статистик представлена в книгах по математической статистике и литературе по анализу данных, например [23],[24],[25],[6]. Однако для полноты представления о методах исследований рассмотрим некоторые из них, которые нашили широкое применение в широком спектре исследовательских задач.
Среднее - сумма значений переменной, деленная на n (число значений переменной).
Мода - наиболее часто встречающееся значение переменной.
Медиана - значение, которое разбивает выборку значений переменной на две равные части: одна половина значений переменной лежит ниже медианы, другая - выше. Расчет медианы выполняется следующим образом. Значения переменной упорядочиваются (полученная последовательность называется вариационным рядом). При нечетном значении числа наблюдений медиана определяется как среднее число в ряду значений переменной или как среднее арифметическое двух средних чисел.
Максимум и минимум определяются по вариационному ряду 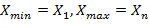 .
.
Дисперсия выборки или выборочная дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формуле:
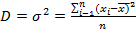 , где (6.1)
, где (6.1)
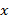 - значение признака;
- значение признака;
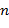 - число наблюдений в выборке.
- число наблюдений в выборке.
Дисперсия характеризует степень разброса количественных измерений статистической выборки (случайных величин) относительно среднего значения для этой выборки.
Стандартное отклонение (в статистике этот показатель еще называют среднеквадратическим отклонением) характеризует степень отклонения данных наблюдений или множеств от среднего значения и имеет вид:
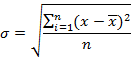
Частота - показатель, показывающий, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
Выбор статистик определится задачами исследования и свойствами выборки. Например, среднее значение, в отличие от медианы, чувствительно к выбросам, что позволяет именно медиану использовать в статистике США в качестве оценки центральной точки доходов населения.
 Рассмотрим пример использования статистик для оценки лояльность к новому виду продукции двумя категориями покупателей: мужчинами и женщинами. В двух выборках, состоящих соответственно из 100 мужчин и 100 женщин, был проведен опрос с целью оценки качества нового вида продукта. Оценки давались в 7-балльной шкале (от 1 - “Совсем не нравится” до 7 - “Очень нравится”). Полученные оценки представлены в двух таблицах, приведенных на рис.6.1. Основываясь на полученных данных необходимо определить, какой из двух сегментов рынка (мужчины или женщины) является более предпочтительным для продажи нового вида продукта.
Рассмотрим пример использования статистик для оценки лояльность к новому виду продукции двумя категориями покупателей: мужчинами и женщинами. В двух выборках, состоящих соответственно из 100 мужчин и 100 женщин, был проведен опрос с целью оценки качества нового вида продукта. Оценки давались в 7-балльной шкале (от 1 - “Совсем не нравится” до 7 - “Очень нравится”). Полученные оценки представлены в двух таблицах, приведенных на рис.6.1. Основываясь на полученных данных необходимо определить, какой из двух сегментов рынка (мужчины или женщины) является более предпочтительным для продажи нового вида продукта.
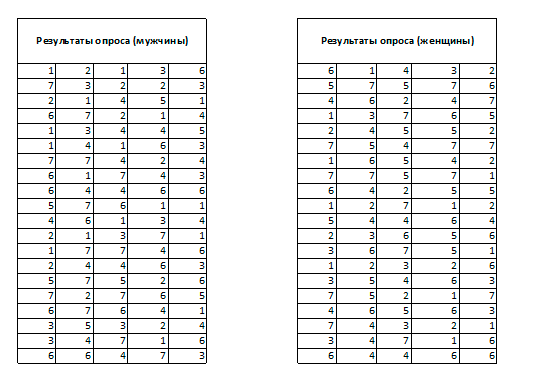
Рис. 6.1. Результаты опросов
Для проведения исследования следует построить распределение частот для различных оценок качества и вычислить итоговые статистические показатели. Частотное распределение оценок целесообразно отобразить графически для обоих сегментов рынка.
Произведенные расчеты позволили получить результаты, представленные на Рис. 6.2, Рис. 6.3, Рис. 6.4. и сделать выводы о целесообразности продажи продукции той или иной категории потребителей.
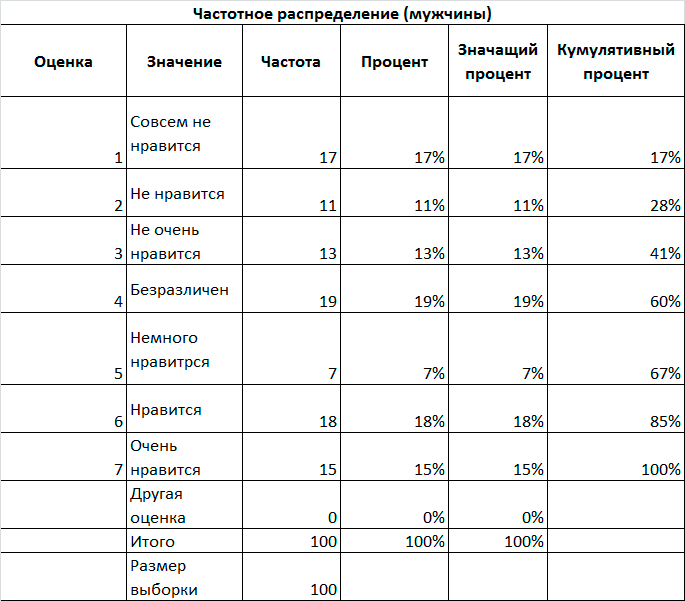 | 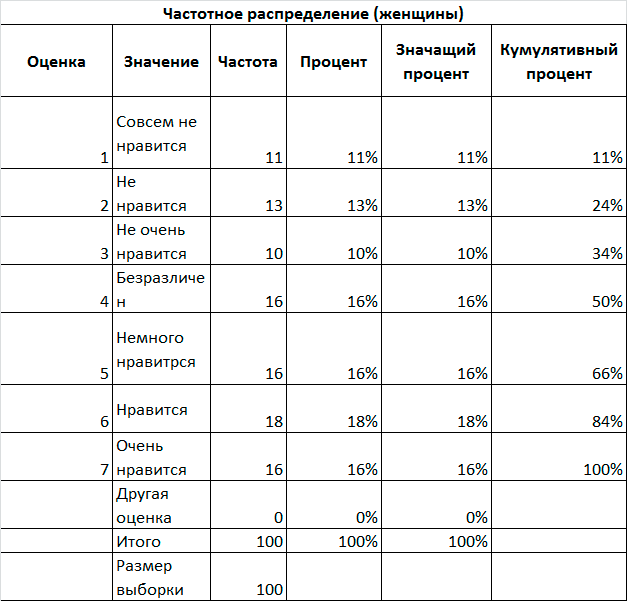 |
Рис. 6.2. Распределение частот отношения респондентов в новому товару
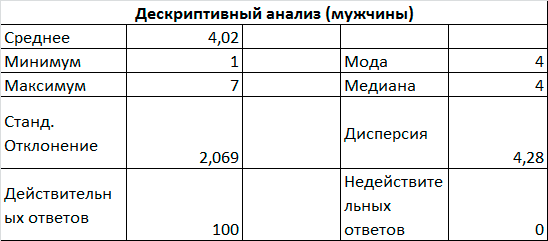 | 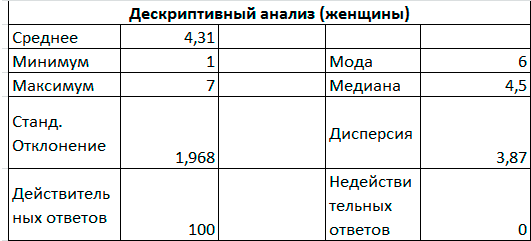 |
Рис. 6.3. Распределение частот отношения респондентов в новому товару
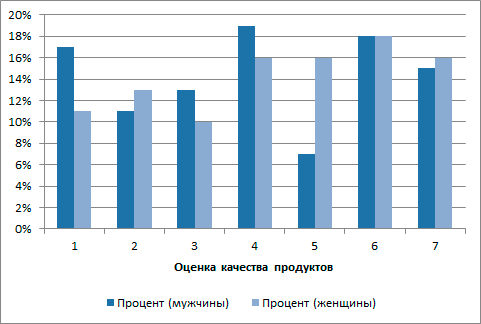
Рис. 6.4. Итоговые статистические показатели
Поскольку наиболее часто встречающимся среди женщин ответом является ответ «Очень нравится», среднее значение ответов превышает значение «Безразличен» и больше чем у мужчин, а частотный анализ показывает большую лояльность к продукции среди женщин, то предпочтительным является предложение данного товара женщинам.
Наибольнейший интерес в статистических исследованиях представляет оценка вероятности того, что переменная примет данное значение из определенного интервала. Соотношение, устанавливающее связь между случайной величиной и соответствующей вероятность называется законом распределения.
Закон распределения может быть представлен в различной форме: в виде ряда распределения, функции распределения, плотности распределения.
Для дискретной величиныряд распределения задается таблицей, содержащей значения случайной величины 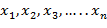 и соответствующие им вероятности
и соответствующие им вероятности 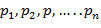 . Для непрерывной случайной величины ряд распределения задается функцией распределения.
. Для непрерывной случайной величины ряд распределения задается функцией распределения.
Функцией распределения случайной величины 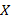 называется функция
называется функция 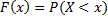 . Функция распределения является неубывающей, причем
. Функция распределения является неубывающей, причем 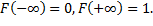 Для дискретных величин функция распределения представляет собой разрывную ступенчатую функцию, а для непрерывных случайных величин - непрерывную функцию.
Для дискретных величин функция распределения представляет собой разрывную ступенчатую функцию, а для непрерывных случайных величин - непрерывную функцию.
Математическое ожидание 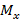 случайной величины рассчитывается по формуле:
случайной величины рассчитывается по формуле:
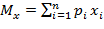 (6.2)
(6.2)
где
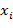 ⎼ случайная величина, которая может принимать случайное значение
⎼ случайная величина, которая может принимать случайное значение 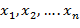 с вероятностями
с вероятностями 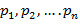
Плотность распределения непрерывной случайной величины есть производная от функции распределения 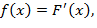 а ее график называется кривой распределения.
а ее график называется кривой распределения.
Наиболее распространённым в практике статистических исследований является нормальное распределение, при котором закон распределения имеет вид:
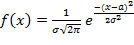 , где (6.3)
, где (6.3)
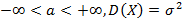 ,
,
 2015-04-01
2015-04-01 13274
13274

 -
-  -
- 






