Определение. Дисперсией случайной величины  называется неотрицательное число
называется неотрицательное число 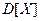 , равное математическому ожиданию квадрата отклонения этой случайной величины от ее математического ожидания:
, равное математическому ожиданию квадрата отклонения этой случайной величины от ее математического ожидания:
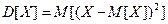 .
.
Таким образом, дисперсия равна:
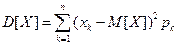 или
или 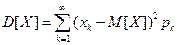 , если случайная величина дискретная;
, если случайная величина дискретная;
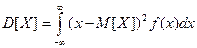 , если случайная величина непрерывна.
, если случайная величина непрерывна.
При этом ряд и несобственный интеграл должны сходиться.
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю: 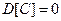 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 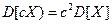 .
.
3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: 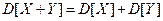 .
.
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: 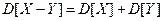 .
.
5. Дисперсия случайной величины удовлетворяет соотношению:
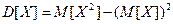 .
.
Определение. Средним квадратическим отклонением 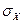 случайной величины
случайной величины  называется корень квадратный из ее дисперсии:
называется корень квадратный из ее дисперсии: 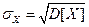 .
.
Пример. Найти дисперсию случайной величины 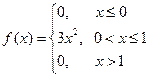 .
.
Решение. Найдем сначала математическое ожидание случайной величины: 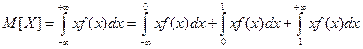 =
= 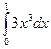 =
= 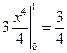 .
.
Дисперсию случайной величины найдем по определению: 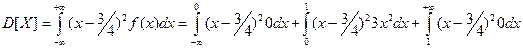 = =
= = 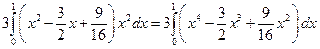 =
= 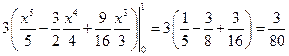 .
.
Пример. Найти дисперсию случайной величины  , которая задана следующим законом распределения:
, которая задана следующим законом распределения: 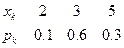 .
.
Решение. Найдем математическое ожидание: 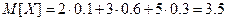 .
.
Запишем закон распределения случайной величины 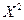 :
:
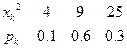
Найдем математическое ожидание квадрата случайной величины: 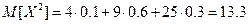 .
.
По свойству 5 дисперсия будет равна:
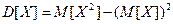 =
= 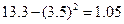 .
.
 2015-04-01
2015-04-01 952
952








