Определение. Функцией распределения случайной величины  называется функция
называется функция 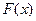 действительной переменной, определяемая равенством:
действительной переменной, определяемая равенством:
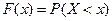 ,
,
где 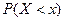 - вероятность того, что случайная величина
- вероятность того, что случайная величина  примет значение, меньшее
примет значение, меньшее 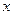 .
.
Свойства функции распределения 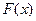 .
.
1. Все значения функции распределения принадлежат отрезку 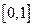 , т.е.
, т.е. 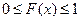 .
.
2. Функция 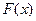 является неубывающей: если
является неубывающей: если 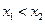 , то
, то 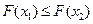 .
.
3. 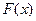 непрерывна слева при любом
непрерывна слева при любом 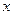 , т.е.
, т.е. 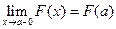 .
.
4. 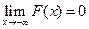 ,
, 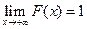 .
.
5. Вероятность того, что случайная величина  примет значение из полуинтервала
примет значение из полуинтервала 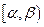 , равна разности значений функции распределения в концах этого промежутка
, равна разности значений функции распределения в концах этого промежутка 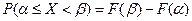 .
.
Функция распределения полностью характеризует случайную величину как дискретную, так и непрерывную. Функцию распределения еще называют интегральным законом распределения.
Функция распределения дискретной случайной величины имеет вид: 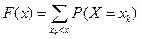 , где выражение
, где выражение 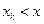 означает, что суммируются вероятности тех значений, которые меньше
означает, что суммируются вероятности тех значений, которые меньше 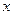 . Такая функция является ступенчатой функцией. Для непрерывной случайной величины функция распределения является непрерывной функцией.
. Такая функция является ступенчатой функцией. Для непрерывной случайной величины функция распределения является непрерывной функцией.
Непрерывная случайная величина может быть охарактеризована еще одной функцией.
Определение. Плотностью распределения случайной величины  называется числовая функция
называется числовая функция  , определяемая соотношением:
, определяемая соотношением: 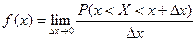 (т.е. предел отношения вероятности того, что значение случайной величины попадет в промежуток
(т.е. предел отношения вероятности того, что значение случайной величины попадет в промежуток 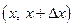 к длине этого промежутка).
к длине этого промежутка).
Свойства плотности распределения  .
.
1. Функция  является неотрицательной:
является неотрицательной: 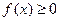 .
.
2. Интеграл по бесконечному промежутку 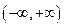 от плотности распределения вероятностей
от плотности распределения вероятностей  равен единице:
равен единице: 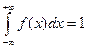 (это свойство называют условием нормировки).
(это свойство называют условием нормировки).
3. В точках дифференцируемости 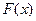 производная функции распределения равна плотности распределения вероятностей:
производная функции распределения равна плотности распределения вероятностей:
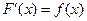 .
.
4. Функция распределения связана с плотностью распределения соотношением: 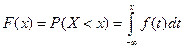 .
.
5. Вероятность попадания значений случайной величины  в полуинтервал
в полуинтервал 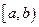 равна определенному интегралу от плотности распределения
равна определенному интегралу от плотности распределения  по отрезку
по отрезку 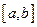 :
: 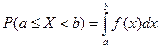 .
.
Свойства 3 и 4 устанавливают связь между функцией распределения и плотностью распределения. Плотность распределения еще называют дифференциальным законом распределения.
Пример. Случайная величина  задана функцией распределения
задана функцией распределения 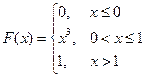 .
.
Найти плотность распределения  , построить графики функций
, построить графики функций 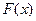 и
и  .
.
Решение. Используя свойство 3, находим: 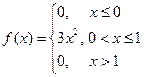 .
.
Графики функций  и
и 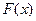 изображены на Рис.4 и 5.
изображены на Рис.4 и 5.
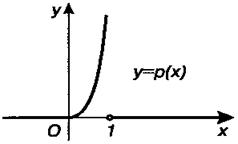
Рис. 4
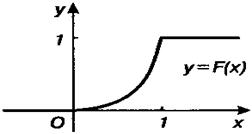
Рис. 5
Пример. Найти функцию 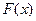 для дискретной случайной величины, закон распределения которой задан таблицей:
для дискретной случайной величины, закон распределения которой задан таблицей: 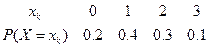 .
.
Решение. Так как случайная величина является дискретной, то функцию 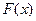 строим, используя формулу
строим, используя формулу 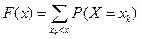 .
.
При 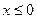
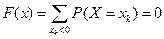 .
.
Если 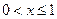 , то
, то 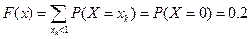 .
.
При 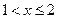 :
: 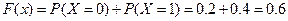 .
.
Если 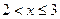 : то
: то 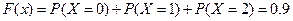 .
.
При 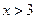 :
: 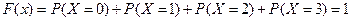 .
.
График функции 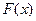 изображен на Рис. 6.
изображен на Рис. 6.
 |
Рис. 6
Пример. Для случайной величины  известна плотность распределения
известна плотность распределения 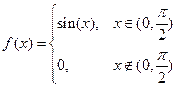 . Требуется найти функцию распределения
. Требуется найти функцию распределения  .
.
Решение. Будем использовать свойство 4 плотности распределения.
Рассмотрим следующие промежутки:
Пусть 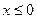 , тогда
, тогда 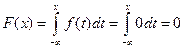 ;
;
Пусть 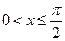 , тогда
, тогда 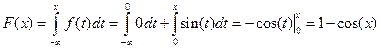 ;
;
Пусть 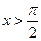 , тогда
, тогда 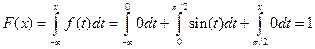 .
.
Окончательно, получаем: 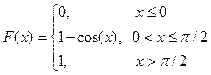 .
.
 2015-04-01
2015-04-01 15653
15653
