|
|
Рассмотрим нахождение производных сложных функций на конкретных примерах.
Пример 5. Найдите производную функции 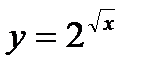 .
.
Решение. Функция 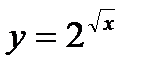 - сложная функция. Обозначим
- сложная функция. Обозначим 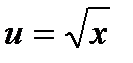 и придем к показательной функции
и придем к показательной функции 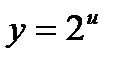 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:
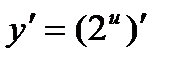 =
= 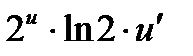 . Заменяя и через
. Заменяя и через 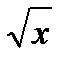 придем к производной вида:
придем к производной вида:
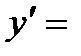
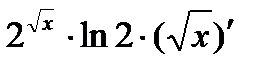 =
= 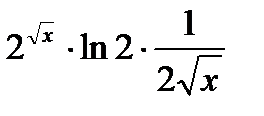 =
= 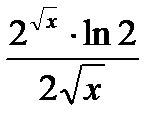 .
.
Ответ: 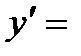
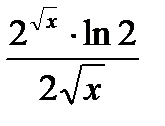 .
.
Пример 6. Найдите производную функции 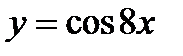 .
.
Решение. Функция 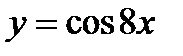 - сложная функция. Обозначим
- сложная функция. Обозначим 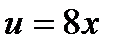 и придем к тригонометрической функции
и придем к тригонометрической функции 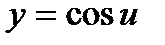 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций:
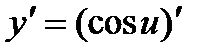 =
= 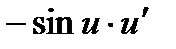 =
= 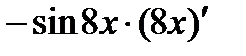 =
= 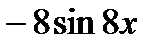 .
.
Ответ: 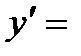
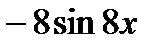 .
.
Пример 7. Найдите производную функции 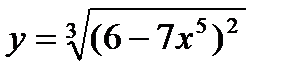 в точке
в точке 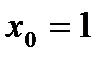 .
.
Решение. Сначала продифференцируем данную функцию. Функция 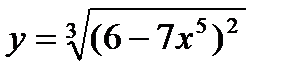 - сложная функция.Представим исходную функцию в виде степени:
- сложная функция.Представим исходную функцию в виде степени: 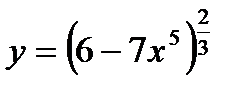 . Обозначим
. Обозначим 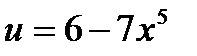 и придем к степенной функции вида
и придем к степенной функции вида 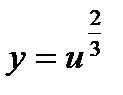 . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 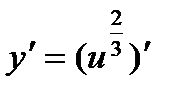 =
= 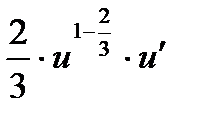 =
= 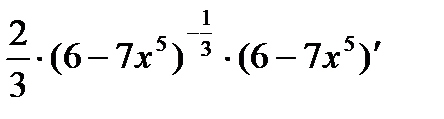 =
= 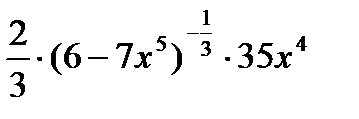 =
= 
= 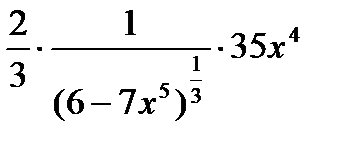 =
= 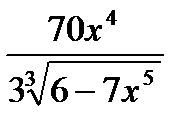 . Итак,
. Итак, 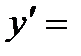
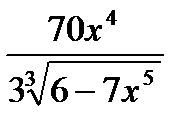 .
. 

Затем в найденную производную 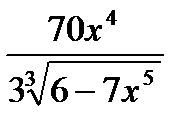 вместо аргумента подставим
вместо аргумента подставим 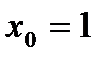 . Получим:
. Получим: 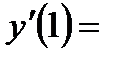
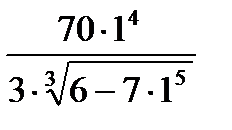 =
= 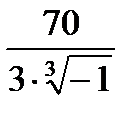 =
= 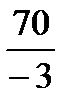 =
= 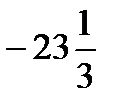 .
.
Ответ: 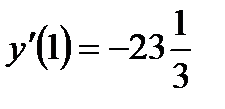 .
.
Пример 8. Найдите производную функции у=arcsinе2х .
Решение. Функция 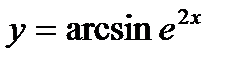 - сложная функция. Обозначим
- сложная функция. Обозначим 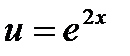 и придем к обратной тригонометрической функции
и придем к обратной тригонометрической функции  . Найдем ее производную по таблице производных сложных функций:
. Найдем ее производную по таблице производных сложных функций: 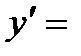 (arcsin u)' =
(arcsin u)' = 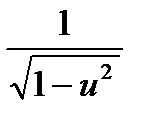 ·u' =
·u' = 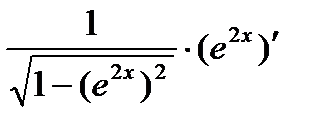 .
.
Однако, мы видим, что е2х тоже сложная функция. Обозначив 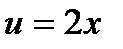 и придя к показательной функции
и придя к показательной функции 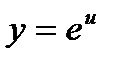 , найдем её производную по таблице производных сложных функций:
, найдем её производную по таблице производных сложных функций: 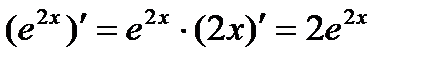 (здесь мы применили краткую запись решения).
(здесь мы применили краткую запись решения).
Получили, что 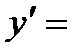
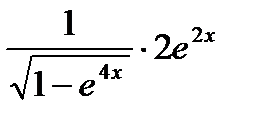 =
= 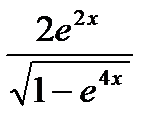 .
.
Ответ: 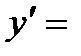
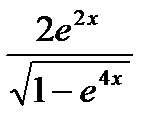 .
.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.1, стр. 116 – 121.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 33, стр. 205-210; § 36, стр.211-217; § 44, стр.240-245.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §4, стр. 208– 228; §6, стр. 245– 247.
 2015-04-01
2015-04-01 1167
1167

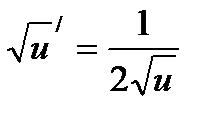 ·u'
·u' 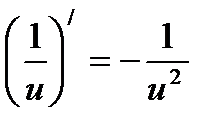 ·u'
·u' 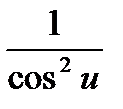 ·u'
·u' 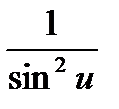 ·u'
·u' 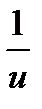 ·u'
·u' 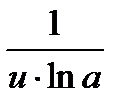 ·u'
·u' 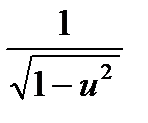 ·u'
·u' 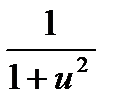 ·u'
·u' 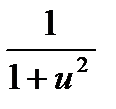 ·u'
·u'