2015-04-01
2064
Пусть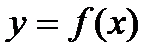 
- дифференцируемая на интервале 
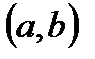функция. Тогда ее производная 
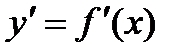- тоже функция, определенная на интервале 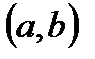. И у нее можно найти производную, называемую производной второго порядка или второй производной. Итак, производная от первой производной 
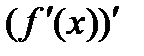называется второй производной функции и обозначается 
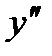или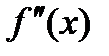 
.
Пример 1. Найдите вторую производную функции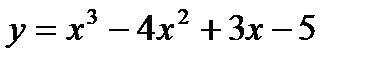 
.
Решение. Найдем у':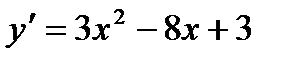 
.
Найдем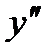 
как производную от у': = 
.
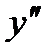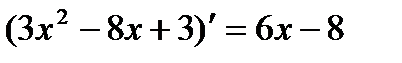Ответ: =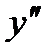 
.
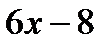Вторая производная – тоже представляет собой функцию, следовательно, существует производная второй производной (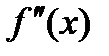
) ', называемая третьей производной или 
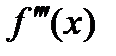. Так, в примере 1. 
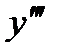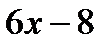=() ' =6.
Аналогично вводится определение четвертой производной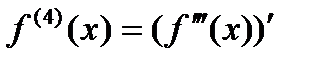 
;
пятой производной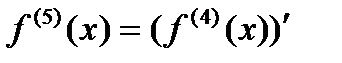 
;
п -й производной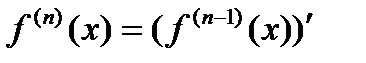 
.
Таким образом, производной п-го порядка функции 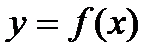называется производная от производной (п -1)-го порядка (если она существует).
Пример 2. Найдите четвертую производную функции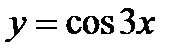 
.
Решение. Найдем у' как производную сложной функции (и=3х):
.
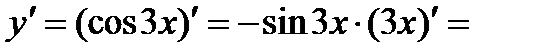
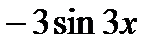Найдем 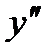как производную от у': =(
) ' = 
= 
.
=(
) ' = 
.
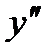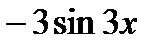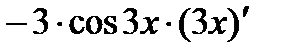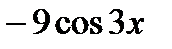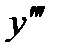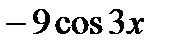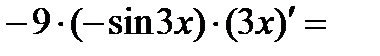
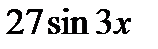у (4)=(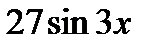
) ' = 
= 
.
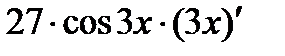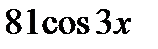Ответ: у (4)=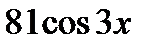 
.
Пример 3. Найдите п -ю производную функции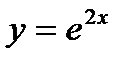 
.
Решение. Найдем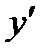 
как производную сложной функции (и=2х):
= 
= 
.
=(
) ' = 
= 
.
=(
) ' = 
= 
.
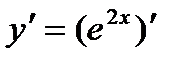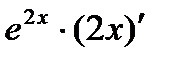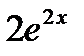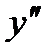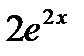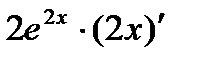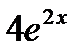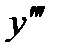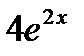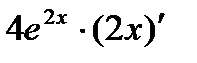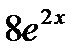Очевидно, что у (п)=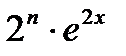 
.
Ответ: у (п)=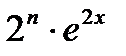 
.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 6, §6.5, стр. 132 – 134.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 37, стр. 218-220.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §5, стр. 239– 240.
