Замечательные пределы. Вычисление пределов с помощью замечательных

Вычисление пределов функции можно осуществлять с помощью замечательных пределов:

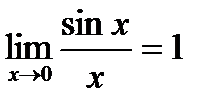- первый замечательный предел;

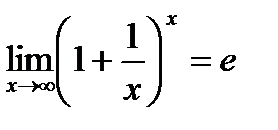- второй замечательный предел.

Пример 7. Вычислите .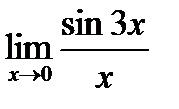

Решение. Поскольку под знаком синуса стоит угол 3 х, домножим числитель и знаменатель дроби на 3, чтобы выражение под знаком синуса и выражение в знаменателе стали равны: .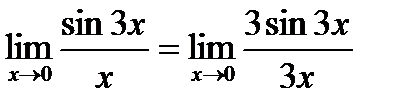

Вынесем число 3 за знак предела: .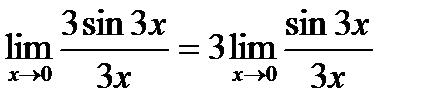

Применив первый замечательный предел, получим, что .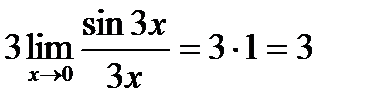

Ответ: 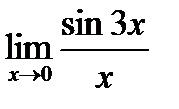=3.

Пример 8. Вычислите .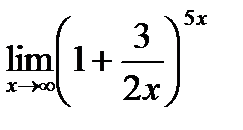

Решение. Постараемся преобразовать выражение под знаком предела таким образом, чтобы прийти ко второму замечательному пределу. Необходимо, чтобы числитель дроби 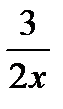был равен 1. Для этого разделим числитель и знаменатель данной дроби на 3; получим дробь вида: 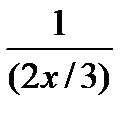. Теперь постараемся преобразовать показатель степени 5 х таким образом, чтобы в нем можно было выделить множитель (2 х /3). Для этого 5 х домножаем на 2 и 3 и делим на 2 и 3:

.

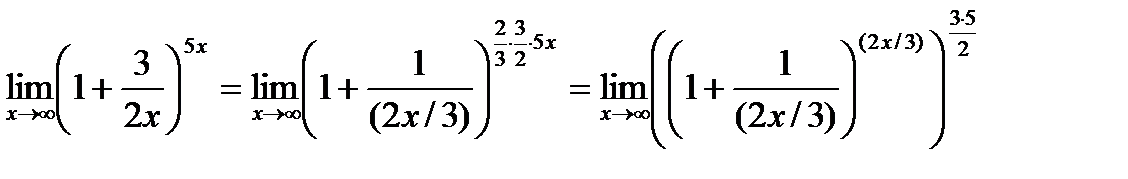е

Применив к выражению в скобках второй замечательный предел, получим, что .

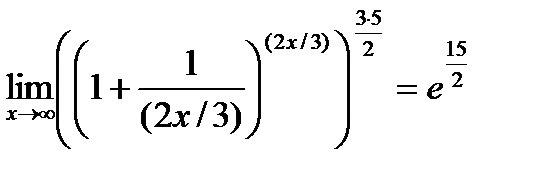Ответ: =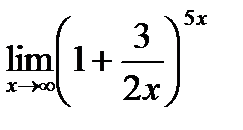

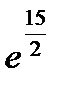
Список литературы:

1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 5, §5.2, стр. 99 – 102.

2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 6, § 31, стр. 188-198.

3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §2, стр. 182 – 192.