Цель: формирование умения вычислять односторонние пределы, находить точки разрыва функции и классифицировать их.
Задание для самостоятельной внеаудиторной работы:
& 13.1.Выучите определения односторонних пределов функции в точке и проанализируйте, как они вычисляются.
?13.2. Вычислите односторонние пределы функции в указанной точке:
а) 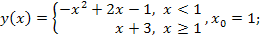 | б) 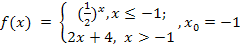 ; ; |
в) 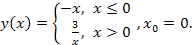 |
& 13.3.Выучите определения непрерывной в точке и на отрезке функции, точки разрыва функции. Изучите классификацию точек разрыва функции. Выясните, какая техника позволяет находить и классифицировать точки разрыва функции.
?13.4. Найдите точки разрыва и определите их род для функции, заданной графически:
|
| ||
|
¶13.5. Исследуйте функцию на непрерывность в указанных точках. Если точка является точкой разрыва функции, определите ее род:
а) 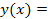
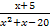 ,
, 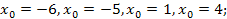
б) 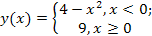 ,
, 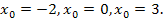
?13.6. Найдите и классифицируйте точки разрыва для функции:
а) 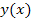 = = 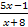 ; ; | б) 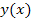 = = 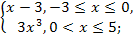 |
в) 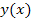 = = 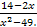 |
¶ 13.7. Выясните, при каком значении параметра 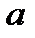 функция
функция 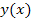 =
= 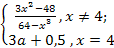 будет непрерывной на всей области определения.
будет непрерывной на всей области определения.
Методические указания по выполнению работы:
При решении задач на нахождение и классификацию точек разрыва функции одним из главных умений является умение вычислять односторонние пределы функции: левосторонний и правосторонний.
Если при нахождении предела функции выбирать значения переменной х только слева от точки хо, то такой предел называется левосторонним и обозначается 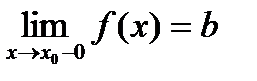 .
.
Если при нахождении предела функции выбирать значения переменной х только справа от точки хо, то такой предел называется правосторонним и обозначается 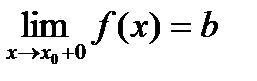 .
.
Функция имеет в точке единый предел тогда и только тогда, когда в этой точке существуют как правосторонний, так и левосторонний пределы, и они равны.
Пример 1. Вычислите односторонние пределы функции
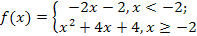 в точке
в точке 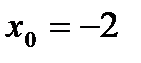 .
.
Решение. Для нахождения левостороннего предела функции в точке 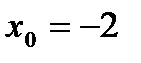 будем выбирать значения переменной, меньшие -2. Но при
будем выбирать значения переменной, меньшие -2. Но при 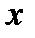 <-2 наша функция задается формулой
<-2 наша функция задается формулой 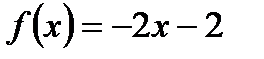 . Таким образом, получим:
. Таким образом, получим: 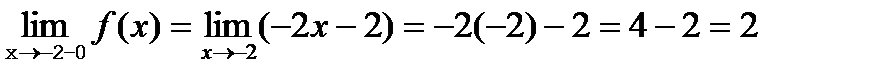 .
.
При нахождении правостороннего предела функции в точке 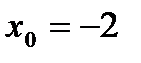 будем выбирать значения переменной, большие -2. Но при
будем выбирать значения переменной, большие -2. Но при 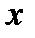 > -2 наша функция задается формулой
> -2 наша функция задается формулой 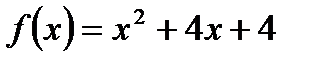 . Таким образом, получим:
. Таким образом, получим: 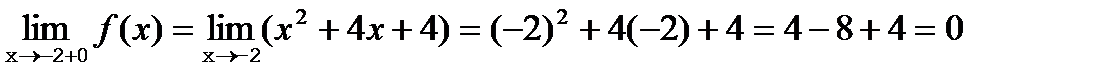 .
.
Ответ 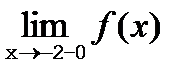 =2,
=2, 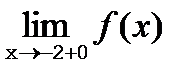 =0.
=0.
Функция у=f(x) называется непрерывной в точке хо, если она определена в ней, существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 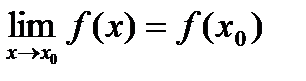 .
.
Функция у=f(x) называется непрерывной на промежутке (a; b), если она непрерывна в каждой точке этого промежутка.
Все элементарные функции (основные элементарные и полученные из них путем выполнения конечного числа арифметических операций или составления сложных функций) непрерывны на области определения.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Все точки разрыва функции подразделяются на точки разрыва первого и второго рода.
Точка разрыва хо называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е. 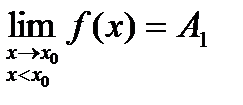 и
и 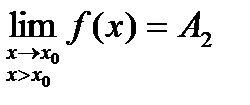 . Если А1 = А2, то точка хо называется точкой устранимого разрыва.
. Если А1 = А2, то точка хо называется точкой устранимого разрыва.
Точка разрыва хо называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел не существует или равен бесконечности.
Пример 2. Найдите точки разрыва и определите их род
| 1 |
| х |
| у |
| 0 |
| 1 |
| 2 |
| · |
| у=g(x) |
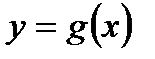 , заданной графически:
, заданной графически: Решение: Непрерывность функции 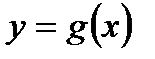 нарушена в единственной точке
нарушена в единственной точке 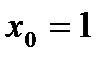 . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке:
. Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: 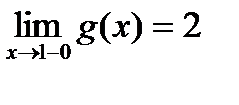 и
и 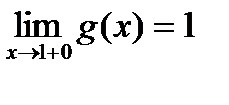 . Они существуют и конечны. Следовательно, точка
. Они существуют и конечны. Следовательно, точка 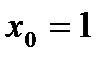 является точкой разрыва I рода функции. Поскольку односторонние пределы не равны друг другу, точка
является точкой разрыва I рода функции. Поскольку односторонние пределы не равны друг другу, точка 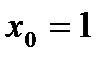 будет точкой устранимого разрыва.
будет точкой устранимого разрыва.
| 1 |
| х |
| у |
| 0 |
| 1 |
| 2 |
| у=f(x) |
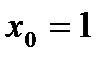 - точка разрыва функции I рода (точка устранимого разрыва).
- точка разрыва функции I рода (точка устранимого разрыва). Пример 3. Найдите точки разрыва и определите их род для функции 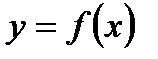 , заданной графически:
, заданной графически:
Решение: Непрерывность функции 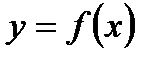 нарушена в единственной точке
нарушена в единственной точке 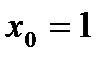 . Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке:
. Она будет точкой разрыва функции. Определим ее род. Для этого по графику найдем односторонние пределы функции в этой точке: 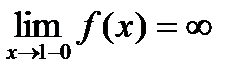 и
и 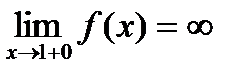 . Они существуют, и оба равны бесконечности. Следовательно, точка
. Они существуют, и оба равны бесконечности. Следовательно, точка 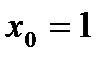 является точкой разрыва II рода функции.
является точкой разрыва II рода функции.
Ответ: 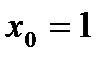 - точка разрыва функции II рода.
- точка разрыва функции II рода.
Если функция задана аналитически, для нахождения и классификации ее точек разрыва удобно использовать следующую технику:
1) выясните, является ли функция элементарной (если да, то она непрерывна на своей области определения);
2) найдите область определения функции и исследуйте на разрыв точки, не принадлежащие ей (но находящиеся внутри области); если перед Вами – функция – скобка, обратите внимание на повторяющуюся в способе задания точку;
3) найдите односторонние пределы функции в каждой из таких точек и в зависимости от этого классифицируйте разрыв (если односторонние пределы существуют и конечны, в точке - разрыв I рода; если хотя бы один из этих пределов не существует или равен бесконечности, в точке – разрыв II рода).
Пример 4. Найдите точки разрыва функции у= 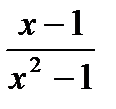 и определите их род.
и определите их род.
Решение. Функция у= 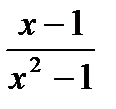 является элементарной, следовательно, она непрерывна на области определения.
является элементарной, следовательно, она непрерывна на области определения.
Найдем D (у): х2 -1≠0; х ≠1 и х ≠-1. Получили, что точки 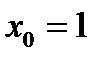 и
и 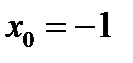 являются точками разрыва функции. Для того, чтобы их классифицировать, найдем односторонние пределы функции в указанных точках.
являются точками разрыва функции. Для того, чтобы их классифицировать, найдем односторонние пределы функции в указанных точках.
Для точки 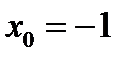
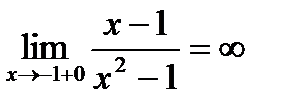 , следовательно,
, следовательно, 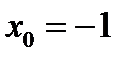 - точка разрыва II рода.
- точка разрыва II рода.
Для точки 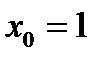
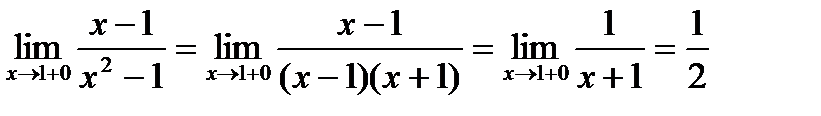 ,
,
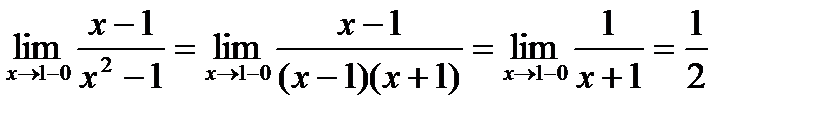 . Следовательно,
. Следовательно, 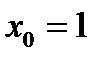 - точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то
- точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то 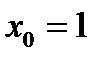 – точка устранимого разрыва. Положив у=
– точка устранимого разрыва. Положив у= 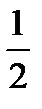 при
при 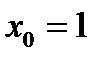 , разрыв устранится, функция станет непрерывной.
, разрыв устранится, функция станет непрерывной.
Ответ: 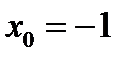 - точка разрыва функции II рода,
- точка разрыва функции II рода,
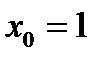 - точка разрыва функции I рода.
- точка разрыва функции I рода.
Пример 5. Найдите точки разрыва функции у= 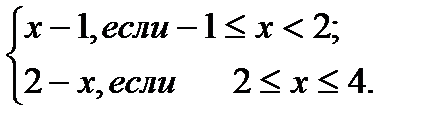 и определите их род.
и определите их род.
Решение. Функция у= 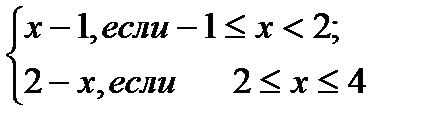 состоит из двух частей: у=х-1 (при
состоит из двух частей: у=х-1 (при 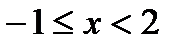 ) и у=2-х (при
) и у=2-х (при 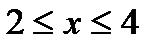 ). Функции у=х-1 и у=2-х являются элементарными, непрерывными на множестве R.
). Функции у=х-1 и у=2-х являются элементарными, непрерывными на множестве R.
Имеет ли функция у= 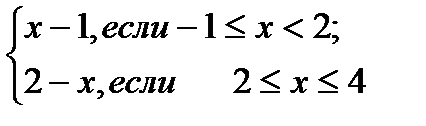 разрыв? Она определена во всех точках отрезка [-1; 4]. Найдем односторонние пределы данной функции в точке
разрыв? Она определена во всех точках отрезка [-1; 4]. Найдем односторонние пределы данной функции в точке 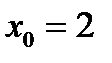 .
.
Левосторонний предел: 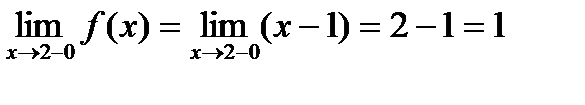 .
.
Правосторонний предел: 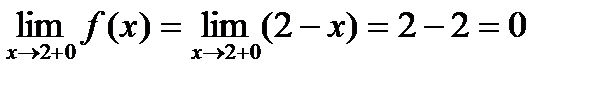 .
.
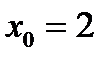 – точка разрыва I рода.
– точка разрыва I рода. Ответ: 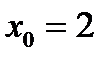 – точка разрыва функции I рода.
– точка разрыва функции I рода.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 5, §5.4, стр. 106 – 110.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 6, § 32, стр. 199-204.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §2, стр. 186 – 190.
 2015-04-01
2015-04-01 1614
1614
