Пример. Косвенным МНК идентифицировать СФМ:
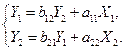
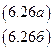
Пусть по экспериментальным данным обычным МНК произведена оценка ПФМ, соответствующей СФМ (6.26):
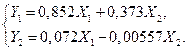

Так как уравнение (6.26 а) не содержит переменной 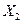 , для исключения
, для исключения 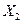 из (6.27 а) находим
из (6.27 а) находим 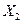 из (6.27 б)
из (6.27 б)
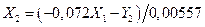
и подставляем в (6.27 а):
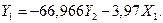
Аналогично для нахождения уравнения (6.26 б) из (6.27 а) находим 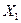 :
:
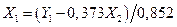
и подставляем в (6.27 б):
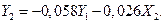
Пример. Косвенным МНК идентифицировать СФМ
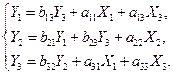
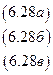
Пусть ПФМ для СФМ (6.28), идентифицированная обычным МНК, имеет вид:
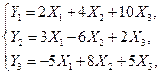
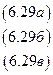
Определение уравнения (6.28 а). Поскольку это уравнение не содержит 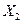 , эту переменную нужно выразить через входящие в уравнение (6.28 а) переменные
, эту переменную нужно выразить через входящие в уравнение (6.28 а) переменные 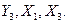 Для этого из уравнения (6.29 в) находим
Для этого из уравнения (6.29 в) находим 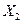
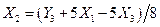
и подставляем в (6.29 а)
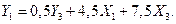
Определение уравнения (6.28 б). Это уравнение не содержит 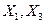 , поэтому их нужно выразить через
, поэтому их нужно выразить через 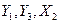 , входящие в это уравнение.
, входящие в это уравнение.
Находим 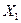 из (6.29 а):
из (6.29 а):
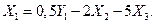 (6.30)
(6.30)
Т. к. (6.30) содержит 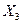 , находим
, находим 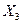 из (6.29 в)
из (6.29 в)
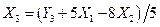
и подставляем в (6.30)
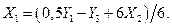 (6.31)
(6.31)
Теперь выразим 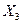 через
через 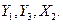
Найдем 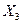 из (6.29 в)
из (6.29 в)
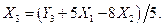 (6.32)
(6.32)
Для исключения 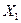 подставляем в (6.32) (6.30):
подставляем в (6.32) (6.30):
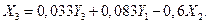 (6.33)
(6.33)
Подставляя (6.31), (6.33) в (6.29 б), получаем (6.28 б):
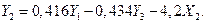
Для определения (6.28 в) выражаем 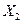 из (6.29 б)
из (6.29 б)
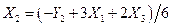
и подставляем в (6.29 в):
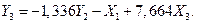
Пример. Двухшаговым МНК идентифицировать СФМ:
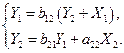
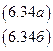
Уравнение (6.34 а) сверхидентифицируемо, т. к. 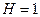
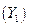 ; (
; (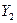 не считается, т. к. входит в уравнение с тем же коэффициентом, что и
не считается, т. к. входит в уравнение с тем же коэффициентом, что и 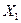 ).
). 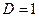
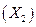 .
. 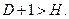
Уравнение (6.34 б) точно идентифицируемо. 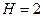
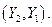
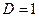
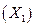 .
. 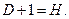
Пусть по тем же экспериментальным данным получена ПФМ, соответствующая СФМ (6.34):
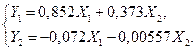

Находя по уравнению (6.35 б) предсказанное значение переменной 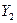 и заменяя в (6.34 а)
и заменяя в (6.34 а) 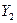 на
на 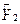 можем идентифицировать (6.34 а) обычным МНК:
можем идентифицировать (6.34 а) обычным МНК:
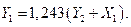
Уравнение (6.34 б) определяем, находя 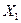 из (6.35 а) и подставляя его в (6.35 б):
из (6.35 а) и подставляя его в (6.35 б):
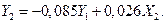
 2015-04-01
2015-04-01 416
416








