Решение показательных неравенств основывается на свойствах монотонности показательной функции 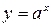 . Напомним, что при
. Напомним, что при 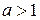 функция строго возрастает, а при
функция строго возрастает, а при 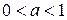 функция убывает.
функция убывает.
Перечислим основные методы решения показательных неравенств.
1. Приведение обеих частей неравенства к одинаковому основанию:
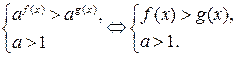 ;
; 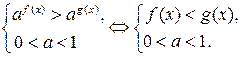
2. Вынесение общего множителя за скобки.
3. Введение новой переменной.
4. Логарифмирование обеих частей неравенства по выбранному основанию.
5. Неравенства вида 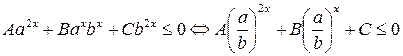 , где
, где 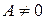 ,
, 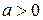 ,
, 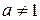 ,
, 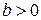 ,
, 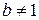 .
.
6. Неравенства вида 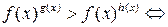
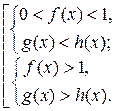
Пример 6.7. Решить уравнение 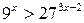 .
.
Решение. Так как 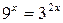 ;
; 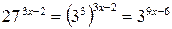 , то, учитывая, что основание
, то, учитывая, что основание 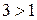 , исходное неравенство перепишется в виде:
, исходное неравенство перепишется в виде:
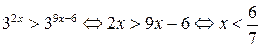
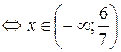 .
.
Ответ: 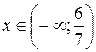 .
.
Пример 6.8. Решить уравнение 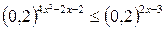 .
.
Решение. Так как основание 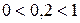 , то
, то
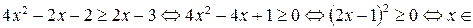
 .
.
Ответ: 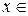
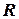 .
.
Пример 6.9. Решить неравенство 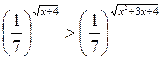 .
.
Решение. Так как основание 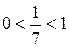 , то
, то
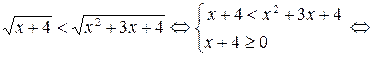
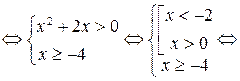
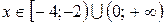 .
.
Ответ: 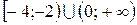 .
.
Пример 6.10. Решить неравенство 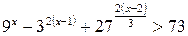 .
.
Решение. 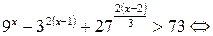
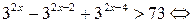
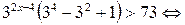
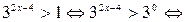
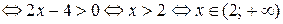 .
.
Ответ: 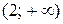 .
.
Пример 6.11. Решить неравенство 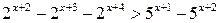 .
.
Решение. 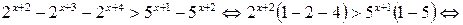
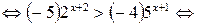
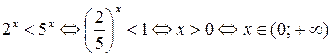 .
.
Ответ: 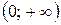 .
.
Пример 6.12. Решить неравенство 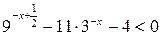 .
.
Решение. 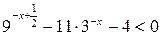
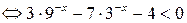 .
.
Сделаем замену 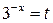 ,
, 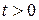 , тогда исходное неравенство примет вид:
, тогда исходное неравенство примет вид:
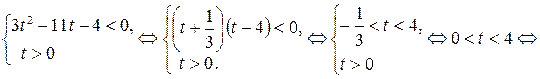
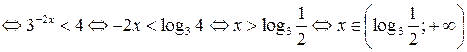 .
.
Ответ: 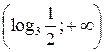 .
.
Пример 6.13. Решить неравенство 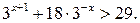
Решение. 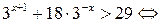
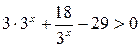 .
.
Сделаем замену: 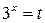 ,
, 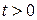 , тогда
, тогда
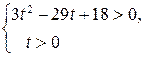
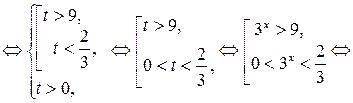
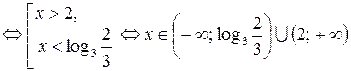 .
.
Ответ: 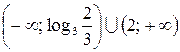 .
.
Пример 6.14. Решить неравенство: 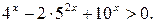
Решение. 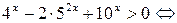
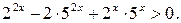
Разделим обе части неравенства на 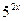 , получаем
, получаем 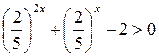 .
.
Сделаем замену  , тогда
, тогда
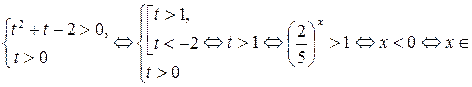
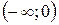 .
.
Ответ: 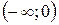 .
.
Пример 6.15. Решить неравенство: 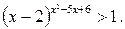
Решение: Исходное неравенство равносильно совокупности двух систем:
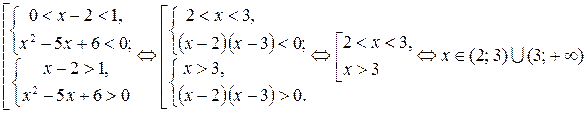 .
.
Ответ: 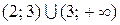 .
.
Пример 6.16. Решить неравенство: 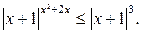
Решение. 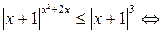
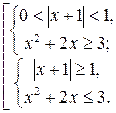
Решим первую систему полученной совокупности:
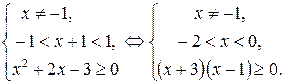
Данная система решений не имеет.
Решим вторую систему совокупности:
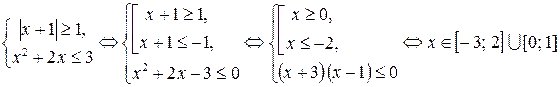 .
.
Ответ: 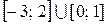 .
.
Пример 6.17. Решить неравенство 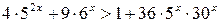 .
.
 2015-04-01
2015-04-01 1432
1432
