Показательные уравнения и неравенства
Определение 6.1. Показательными называется уравнения, у которых переменная содержится в показатели степени.
Рассмотрим основные методы решения показательных уравнений.
1. Приведение обеих частей уравнения к одинаковому основанию:
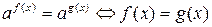 , где
, где 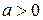 ,
, 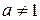 .
.
2. Вынесение общего множителя за скобки.
3. Уравнения, в которых правая и левая часть не приводится к одному основанию, можно решить логарифмированием:
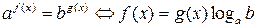 .
.
4. Введение новой переменной.
5. Уравнение вида 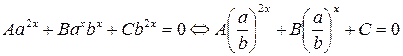 , где
, где 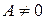 ,
, 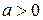 ,
, 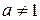 ,
, 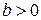 ,
, 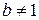 .
.
6. Показательно-степенные уравнения 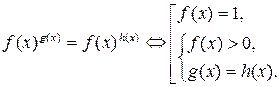
7. Функциональный метод.
Пример 6.1. Решить уравнение 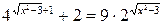 .
.
Решение. 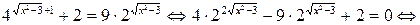
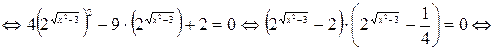
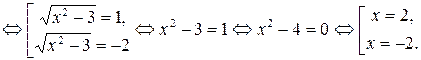
Ответ: 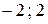 .
.
Пример 6.1. Решить уравнение 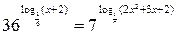 .
.
Решение. Найдем предварительно ОДЗ уравнения:
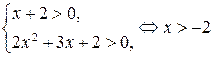 .
.
Тогда на ОДЗ получим:
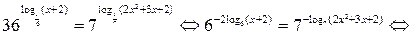
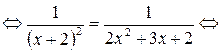
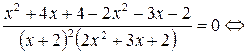
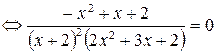
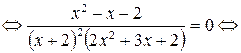
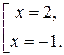
Оба корня принадлежат ОДЗ.
Ответ: 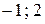 .
.
Пример 6.2. Решить уравнение 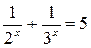 .
.
Решение. Так как левая часть является строго убывающей функцией, то любое положительное значение эта функция принимает ровно один раз. Следовательно, уравнение имеет единственное решение. Подбором получаем, что решением уравнения является 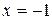 .
.
Ответ: 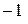 .
.
Пример 6.3. Решить уравнение 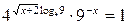 .
.
Решение. Прологарифмируем уравнение по основанию 4:
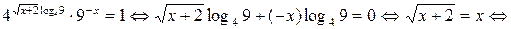
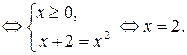
Ответ: 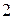 .
.
Пример 6.4. Решить уравнение: 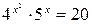 .
.
Решение. Прологарифмируем уравнение, например, по основанию 4. Тогда:
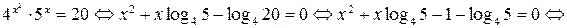
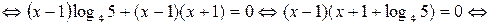
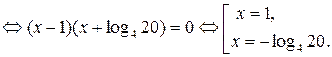
Ответ: 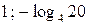 .
.
Пример 6.5. Решить уравнение
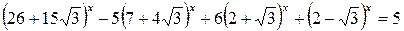 .
.
Решение. Отметим, что
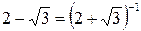 ,
, 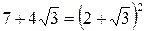 ,
, 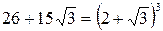 .
.
Введем замену  ,
, 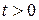 , тогда уравнение примет вид:
, тогда уравнение примет вид:
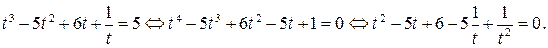
Сделаем замену: 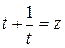 ,
, 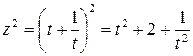 , тогда
, тогда
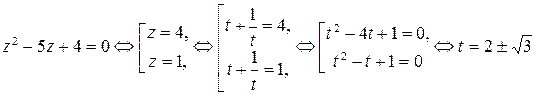 .
.
Переходя обратно к переменной 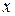 , получаем
, получаем
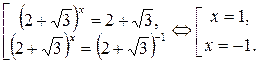
Ответ: 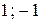 .
.
Пример 6.6. Решить уравнение 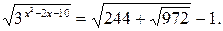
Решение. Проведем предварительно преобразование правой части уравнения
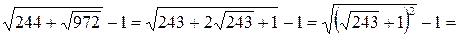
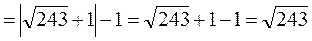 .
.
Тогда исходное уравнение привет вид:
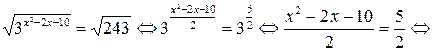
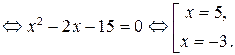
Ответ: 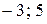 .
.
 2015-04-01
2015-04-01 728
728







