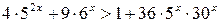
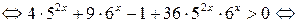 .
.
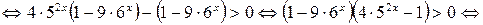 .
.
Последнее неравенство равносильно совокупности двух систем:
1. 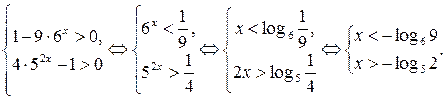
2. 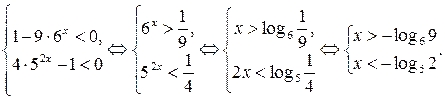
Сравним числа 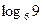 и
и 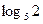 . Так как
. Так как 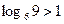 , а
, а 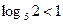 , то
, то  , значит
, значит 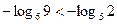 . Тогда получаем, что первая система решений не имеет, а решениями второй служит промежуток
. Тогда получаем, что первая система решений не имеет, а решениями второй служит промежуток 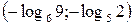 .
.
Ответ: 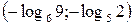 .
.
Пример 6.18. Решить неравенство: 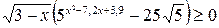 .
.
Решение. Область определения неравенства определяется условием 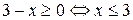 . Исходное неравенство равносильно совокупности:
. Исходное неравенство равносильно совокупности:
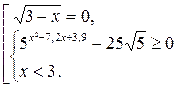 .
.
Из уравнения 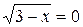 получаем
получаем  .
.
Так как 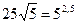 , то первое неравенство системы можно записать в виде
, то первое неравенство системы можно записать в виде
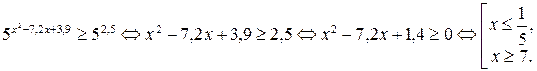
Учитывая условие 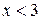 , получаем решение системы – промежуток
, получаем решение системы – промежуток 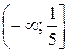 . Тогда решение исходного неравенства имеет вид
. Тогда решение исходного неравенства имеет вид 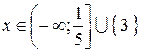 .
.
Ответ: 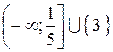 .
.
Пример 6.19. Решить неравенство 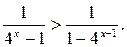
Решение. 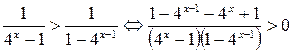 .
.
Сделаем замену 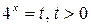 , тогда
, тогда
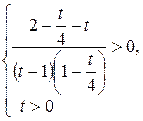
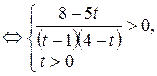
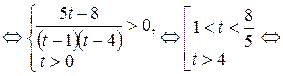
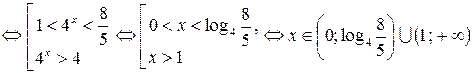 .
.
Ответ: 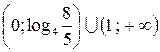 .
.
Задачи для самостоятельного решения
 2015-04-01
2015-04-01 440
440








