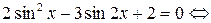
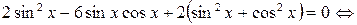
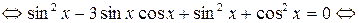
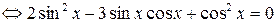 .
.
Последнее уравнение является однородным. Разделив обе части уравнения на 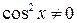 , получим
, получим
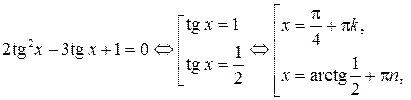
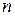 ,
, 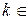
 .
.
Ответ: 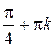 ;
; 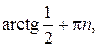
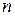 ,
, 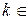
 .
.
Пример 8.26. Решить уравнение 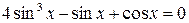 .
.
Решение. Данное уравнение не является однородным. Перепишем его следующим образом: 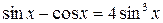 . Умножив обе части уравнения на
. Умножив обе части уравнения на 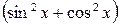 и приведя подобные слагаемые, получим:
и приведя подобные слагаемые, получим:
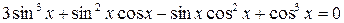 .
.
Разделив обе части уравнения на 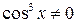 и положив
и положив 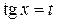 , получим:
, получим: 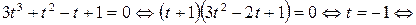
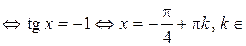
 .
.
Ответ: 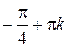 ,
, 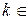
 .
.
Пример 8.27. Решить уравнение 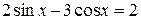 .
.
Решение. Воспользуемся формулами двойного аргумента:
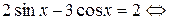
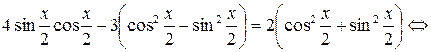
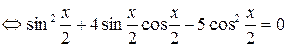 .
.
Разделим обе части уравнения на 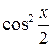 и сделаем замену
и сделаем замену 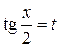 , тогда получим:
, тогда получим:
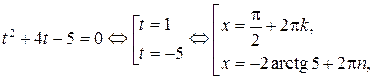
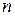 ,
, 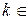
 .
.
Ответ: 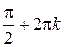 ;
; 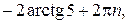
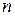 ,
, 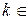
 .
.
Пример 8.28. Решить уравнение 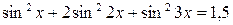 .
.
Решение. Преобразуем исходное уравнение, используя формулы понижения степени (половинного аргумента):
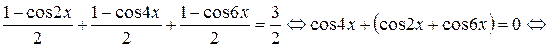
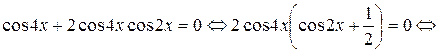
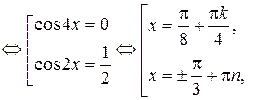
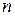 ,
, 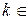
 .
.
Ответ: 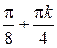 ;
; 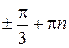
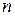 ,
, 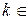
 .
.
Пример 8.29. Решить уравнение 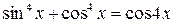 .
.
 2015-04-01
2015-04-01 320
320








