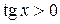 ,
, 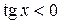 ,
, 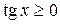 ,
, 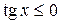
удобно решать сначала на интервале 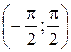 , а неравенства вида
, а неравенства вида
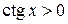 ,
, 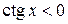 ,
, 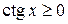 ,
, 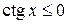 –
–
на интервале 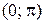 .
.
Так как функции 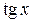 и
и 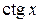 имеют период
имеют период 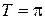 , поэтому прибавляя к найденным на соответствующих интервалах решениям числа вида
, поэтому прибавляя к найденным на соответствующих интервалах решениям числа вида 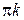 ,
, 
 , получим все решения данных неравенств.
, получим все решения данных неравенств.
Пример 8.33. Решить неравенство 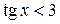 .
.
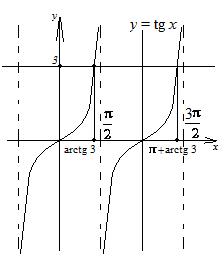 рис. 8.3.
рис. 8.3.
| Решение.На интервале 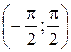 функция функция 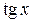 монотонно возрастает и уравнение монотонно возрастает и уравнение  имеет одно решение имеет одно решение 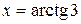 (рис. 8.3). Решениями данного неравенства на всей числовой прямой являются (рис. 8.3). Решениями данного неравенства на всей числовой прямой являются
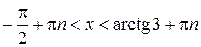 , ,   , ,
|
или 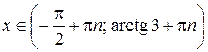 ,
, 
 .
.
Ответ: 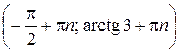 ,
, 
 .
.
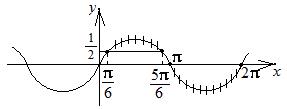
Пример 8.34. Решить неравенство 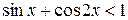 .
.
Решение. Преобразуем выражениев левой части неравенства:
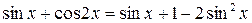 ,
,
тогда
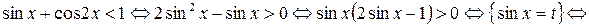
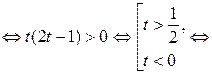
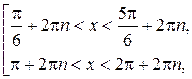

 (рис. 8.4).
(рис. 8.4).
Ответ: 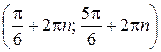 ;
; 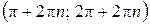

 .
.
| 
|
| рис. 8.4. | рис. 8.5. |
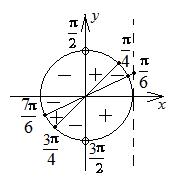
Замечание 8.1. При решении тригонометрических неравенств можно вместо числовой оси использовать числовую окружность, которая корнями тригонометрических уравнений разбивается на дуги. Затем применяется метод интервалов.
Пример 8.35. Решить неравенство 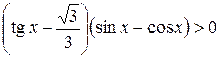 .
.
Решение. ОДЗ 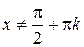 ,
, 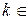
 . Найдем корни уравнения
. Найдем корни уравнения
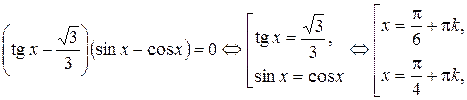
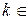
 .
.
Отметим найденные корни и ОДЗ на тригонометрической окружности (рис. 8.5). При переходе через точку, как и в традиционном методе интервалов, знак неравенства меняется на противоположный. Для определения знака, присущего каждой дуге, возьмем, например, точку 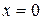 и определим знак неравенства в этой точке:
и определим знак неравенства в этой точке:
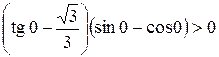 .
.
Тогда решение исходного неравенства имеет вид:
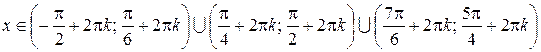 ,
, 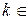
 .
.
Ответ: 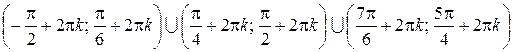 ,
, 
 .
.
 2015-04-01
2015-04-01 470
470








