Определение 8.5. Неравенства, содержащие тригонометрические функции, называются тригонометрическими.
При решение тригонометрических неравенств используют периодичность тригонометрических функций и их монотонность на соответствующих промежутках.
Функции 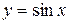 и
и 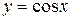 имеют наименьший положительный период
имеют наименьший положительный период 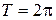 . Поэтому неравенства вида
. Поэтому неравенства вида
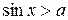 ,
, 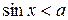 ,
, 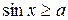 ,
, 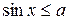 ,
,
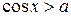 ,
, 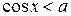 ,
, 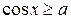 ,
, 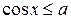
достаточно решить сначала на каком-либо отрезке длины 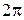 , тогда множество всех решений получим, прибавив к каждому из найденных на этом отрезке решений числа вида
, тогда множество всех решений получим, прибавив к каждому из найденных на этом отрезке решений числа вида 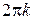 ,
, 
 .
.
Пример 8.32. Решить неравенство 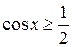 .
.
Решение. На отрезке 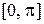 функция
функция 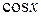 монотонно убывает, а уравнение
монотонно убывает, а уравнение 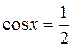 имеет одно решение
имеет одно решение 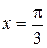 (рис. 8.2)
(рис. 8.2)
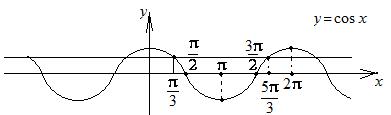 рис. 8.2.
рис. 8.2.
| На отрезке 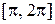 функция функция 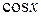 монотонно возрастает, и уравнение монотонно возрастает, и уравнение 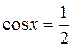 имеет решение имеет решение 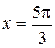 . .
|
Значения 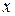 из отрезка
из отрезка 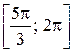 являются решениями данного неравенства на отрезке
являются решениями данного неравенства на отрезке 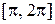 . Таким образом, множество решений неравенства
. Таким образом, множество решений неравенства 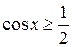 на отрезке
на отрезке 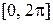 есть объединение отрезков
есть объединение отрезков 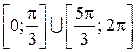 .
.
Функция 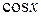 периодична с периодом
периодична с периодом 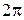 , поэтому все значения
, поэтому все значения 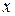 , каждое из которых удовлетворяет неравенствам
, каждое из которых удовлетворяет неравенствам
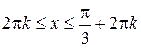 ,
, 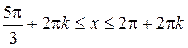 ,
, 
 ,
,
являются решениями исходного неравенства или
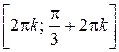
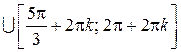 ,
, 
 .
.
Ответ можно записать в более компактном виде:
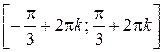 ,
, 
 .
.
 2015-04-01
2015-04-01 298
298








