2015-04-01
827
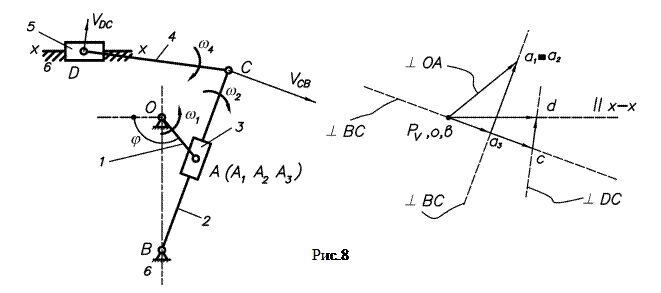
Построить план скоростей для кулисного механизма (рис.8).
Дано: размеры звеньев, угловая скорость ведущего звена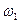 
, положение ведущего звена 
.
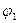1. Звено 1 вращается вокруг т. О с угловой скоростью 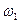, поэтому:
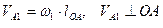
Скорость т. А1 направлена в сторону вращения кривошипа. От полюса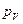 
в масштабе откладываем вектор 
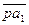, изображающий скорость т. А1.
Точка А1 тождественна точке А2 (в противном случае не было бы передачи движения), А1 = А2. Следовательно,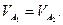 
2. Вектор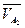 
определен по величине и направлению. С одной стороны, точка А2 совершает вращательное движение относительно точки О (стойки механизма). С другой стороны, точка А2 совершает поступательное движение относительно кулисы (звено 5) и вращательное движение вместе с кулисой вокруг точки В.
Таким образом, точка А2 совершает сложное движение. Абсолютное движение – движение точки А2 относительно неподвижной системы координат (стойки механизма), относительное движение – поступательное движение точки А2 относительно кулисы (относительно точки А3) и переносное движение – вращательное движение кулисы (точки А3) вокруг центра В (стойки механизма).
Для того, чтобы получить величины скоросте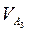й 
и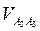 
, направление которых известно, вектор абсолютного движения 
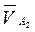необходимо разложить на две составляющие по направлениям векторов 
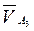и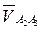 
. Иными словами, можно записать уравнение:
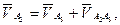
где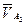 
- вектор скорости т. А2 в абсолютном движении;
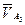- вектор скорости т. А3 в переносном движении, т.е.
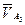- переносная скорость кулисы 3;
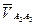- относительная скорость движения т. А2 относительно А3 или
скорость ползуна 2 по кулисе 3.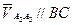 
.
Точка В принадлежит стойке механизма, поэтому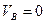 
.
 |
Согласно уравнению: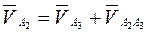 
- вектор скорости т. А2 является результирующим вектором, отложенным на плане скоростей как вектор 
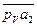, поэтому к результирующему вектору 
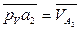пристраиваем два суммируемых вектора – 
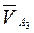и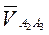 
. Для этого из начала вектора 
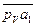(с учетом уравнения 
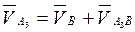) из т. 
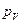– полюса плана скоростей – проводим линию перпендикулярно ВС (направление скорости т. А3 относительно т. В). Линию действия относительной скорости 
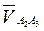проводим из конца вектора 
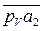– от точки 
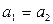. Пересечение указанных линий действия определит точку 
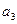– конец вектора 
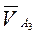. Вектор 
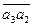будет представлять собой скорость скольжения 
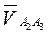. Находим модули скоростей:
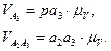
3. Используя частный случай теоремы подобия, определим отрезок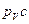 
, изображающий скорость точки С. Запишем соотношение:
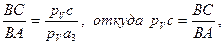
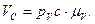
4. Скорость т. D определяется из уравнения:
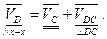
После решения этого уравнения получаем:
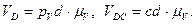
5. Определение угловых скоростей звеньев 3 и 4. Угловая скорость кулисы 3 определяется соотношением:
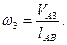
и направлена по часовой стрелке (по направлению скорости VА3), аналогично:
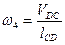– по часовой стрелке.
ПОСТРОЕНИЕ ПЛАНА УСКОРЕНИЙ
