Вычислить объём тела, полученного от вращения вокруг оси ох фигуры, ограниченной линиями у= х2-х-2, х=-1, х=2.
Решение. Сделаем чертёж (рисунок 4). По формуле V= 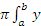 2dx, где а=-1, и=2, находим
2dx, где а=-1, и=2, находим
V= 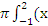 2 –х-2)2 dx=
2 –х-2)2 dx= 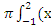 2 –(х+2))2 dx=
2 –(х+2))2 dx= 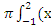 4 –2х3-3х2+4х+4) dx=
4 –2х3-3х2+4х+4) dx=
(х5/5-х4/2 -х3+2х2+4х)׀2-1 = 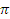 (32/5-8-8+8+8+1/5+1/2-1-2+4)=8,1
(32/5-8-8+8+8+1/5+1/2-1-2+4)=8,1 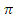 (куб. ед.)
(куб. ед.)
- Как связаны между собой операции нахождения производной и первообразной?
- Перечислите свойства неопределённого интеграла?
- Приведите примеры табличных интегралов.
- Перечислите свойства определённого интеграла?
- Приведите пример экономического приложения определённого интеграла.
- Вычислить интегралы:
a. 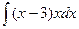
b. 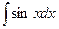
c. 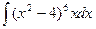
 2015-04-01
2015-04-01 1281
1281








