На практике чаще встречаются не чистые газы, а их смеси. Компоненты смеси занимают один и тот же объем и имеют одинаковую температуру. Концентрация смеси равна сумме концентраций компонентов смеси, т. е.
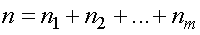 .
.
Тогда по формуле (4.5) давление смеси равно:
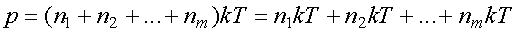 .
.
Введем обозначения:
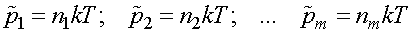 ,
,
где 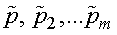 - парциальные давления.
- парциальные давления.
Парциальным давлением называется давление, которое производит на стенки сосуда данная компонента смеси.
Тогда давление смеси равно:
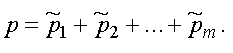 (1.15)
(1.15)
Формула (1.15) представляет собой закон Дальтона. Давление смеси газов равно сумме парциальных давлений.
Основные понятия классической и квантовой статистики
Классическая статистика описывает макросистемы, состоящие из микрочастиц, движение которых в рассматриваемых условиях можно описывать законами классической механики (механики Ньютона). Примером такой системы, подчиняющейся законам классической статистики является идеальный газ.
В общем случае для описания движения микрочастиц, необходимо применять законы квантовой механики. Статистическая физика, описывающая макросистемы, состоящие из микрочастиц, движение которых описывается законами квантовой механики, называется квантовой статистикой.
Одним из основных понятий статистики (как классической, так и квантовой) является вероятность. Пусть какая-либо физическая система может находиться в различных физических состояниях. Предположим, что эти состояния дискретны, т.е. характеризующие их физические величины изменяются скачками и каждое состояние характеризуется определенным значением хi некоторой физической величины х.
В некоторых состояниях система будет проводить большее время, в некоторых – меньшее. Будем измерять величину х некоторое число раз N. Обозначим Ni – число измерений, каждое из которых дает значение измеряемой величины х, равное хi. Вероятность wi того, что величина х имеет значение хi, называется предел отношения числа Ni к полному числу измерений N при стремлении N к бесконечности, т.е.:
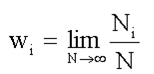 (1.16)
(1.16)
Дискретное значение физических величин - характерная особенность всех микрочастиц (атомов, молекул). Например, энергия вращательного и колебательного движения молекулы может меняться только дискретно, скачками. Про такую величину говорят, что она квантуется.
Вместе с тем, можно с большой точностью считать, что энергия поступательного движения молекул не квантуется, т.е. изменяется непрерывно, значит, непрерывно меняется и скорость молекул газа, а также и координата молекул в пространстве. Для непрерывной случайной величины, например, скорости молекулы v, вероятность dwv того, что скорость молекулы v принимает значения в интервале от v до v + dv вычисляется так:
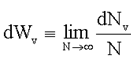 (1.17)
(1.17)
здесь N - полное число измерений скорости, dNv - число измерений, в которых скорость молекулы попали в интервал от v до v + dv.
Очевидно, что:
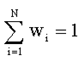 (1.18)
(1.18)
Это следует из определения вероятности (1.17):
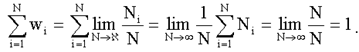
Аналогично и для непрерывной случайной величины. Из (1.18) следует, что:
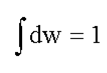 (1.19)
(1.19)
Барометрическая формула
Барометрическая формула дает зависимость давления р идеального газа, находящегося в однородном поле тяжести при постоянной температуре Т, от высоты z:
 (1.20)
(1.20)
где po - давление при z = 0, mo - масса молекулы, k - постоянная Больцмана.
Распределение Больцмана.
Распределение Больцмана позволяет для молекулы, находящейся во внешнем потенциальном поле с энергией εn(x, y, z), найти вероятность dwr того, что эта молекула имеет координаты x, y, z в интервалах dx, dy, dz, соответственно:
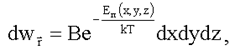 (1.21)
(1.21)
здесь В - постоянный множитель, определяемый из условия нормировки:
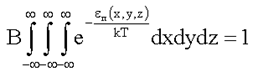 . (1.22)
. (1.22)
Распределение Максвелла.
Молекулы идеального газа, находящегося в термодинамическом равновесии, вполне определенным образом распределены не только по координатам, но и по проекциям своих скоростей. Как найти такое распределение? Во-первых, следует правильно поставить задачу. Например, постановка задачи в виде: определить количество молекул, имеющих ту или иную заданную скорость, не имеет смысла, потому что это количество математически точно равно нулю! В самом деле, количество молекул, входящих в систему, является хотя и большим, но конечным (равно N). В то же время количество различных значений скорости бесконечно. Поэтому число молекул, приходящихся на долю каждого значения скорости, равно нулю (N/∞ → 0).
Правильная постановка задачи: сколько молекул, или какая часть молекул n = ΔN/N будет иметь скорость V, лежащую в интервале скоростей V + ΔV? Именно так и формулируются статистические задачи. Например, какая часть людей в стране (области, районе) имеют возраст в интервале от 20 до 21 года. Или, например, чтобы прогнозировать, сколько школьных форм определенного размера следует пошить, чтобы обеспечить всех школьников данной местности, следует определить, сколько школьников имеют рост от 149 до 151 см.
Статистическую задачу, какая часть молекул n = ΔN/N будет иметь скорость V, лежащую в интервале скоростей V + ΔV, поставил и решил для идеального газа Д.К. Максвелл.
Максвеллом было получено следующее соотношение:
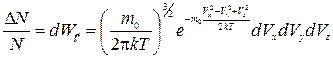 (1.23)
(1.23)
здесь 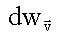 - вероятность обнаружения молекулы в бесконечно малом прямоугольном параллелепипеде в пространстве скоростей, изображенном на рис. 1.3.
- вероятность обнаружения молекулы в бесконечно малом прямоугольном параллелепипеде в пространстве скоростей, изображенном на рис. 1.3.
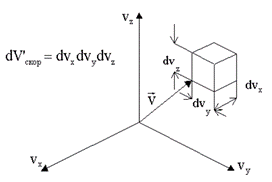
Рис. 1.3
Другими словами, это вероятность того, что молекула имеет проекцию скорости на ось х в интервале от vх до vх + dvх и в подобных же интервалах для значений vy и vz.
Из (1.23) видно, что вероятность 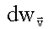 не зависит от направления вектора
не зависит от направления вектора  , а зависит только от его модуля. Поэтому в формуле (1.23) в качестве элементарного объема в пространстве скоростей вместо прямоугольного параллелепипеда можно взять бесконечно тонкий сферический слой (см. рис. 1.4), радиус которого v, а толщина dv. В этом элементарном объеме все модули скоростей с отклонением, не превышающем dv, равны v. Перейдем, таким образом, от dvх, dvy,dvz к 4πv2dv, где 4πv2 - площадь сферы в пространстве скоростей, изображенной на рис. 1.4.
, а зависит только от его модуля. Поэтому в формуле (1.23) в качестве элементарного объема в пространстве скоростей вместо прямоугольного параллелепипеда можно взять бесконечно тонкий сферический слой (см. рис. 1.4), радиус которого v, а толщина dv. В этом элементарном объеме все модули скоростей с отклонением, не превышающем dv, равны v. Перейдем, таким образом, от dvх, dvy,dvz к 4πv2dv, где 4πv2 - площадь сферы в пространстве скоростей, изображенной на рис. 1.4.
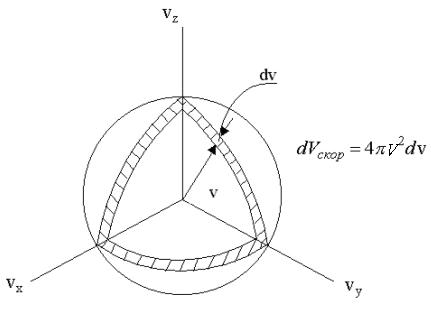
Рис. 1.4.
После чего формула (1.23) принимает вид:
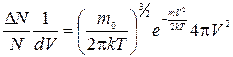 (1.24)
(1.24)
Формулу (1.24) обычно записывают в виде:
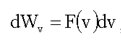 (1.25)
(1.25)
где 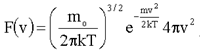 (1.26)
(1.26)
Полученную Д.К. Максвеллом функцию F(v) принято называть функцией распределения вероятностей или функцией распределения Максвелла.
Из (1.25) следует, что:
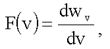
поэтому F(v) называют еще и плотностью вероятности.
График функции распределения Максвелла приведен на рис. 1.5.
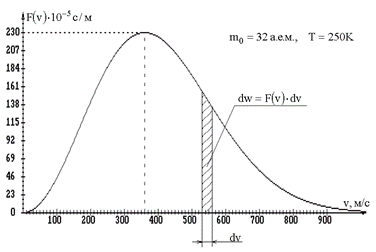
Рис. 1.5.
 2015-04-01
2015-04-01 10988
10988
