В 1920 году физиком Отто Штерном (1888-1969) впервые были экспериментально определены скорости частиц вещества.
Прибор Штерна состоял из двух цилиндров разных радиусов, закрепленных на одной оси. Воздух из цилиндров был откачен до глубокого вакуума. Вдоль оси натягивалась платиновая нить, покрытая тонким слоем серебра. При пропускании по нити электрического тока она нагревалась до высокой температуры, и серебро с ее поверхности испарялось (рис. 1.7).
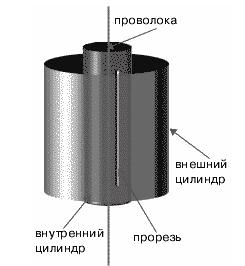
Рис. 1.7. Схема опыта Штерна.
В стенке внутреннего цилиндра была сделана узкая продольная щель, через которую проникали движущиеся атомы металла, осаждаясь на внутренней поверхности внешнего цилиндра, образуя хорошо наблюдаемую тонкую полоску прямо напротив прорези.
Цилиндры начинали вращать с постоянной угловой скоростью. Теперь атомы, прошедшие сквозь прорезь, оседали уже не прямо напротив щели, а смещались на некоторое расстояние, так как за время их полета внешний цилиндр успевал повернуться на некоторый угол (рис. 1.8). При вращении цилиндров с постоянной скоростью, положение полоски, образованной атомами на внешнем цилиндре, смещалось на некоторое расстояние.
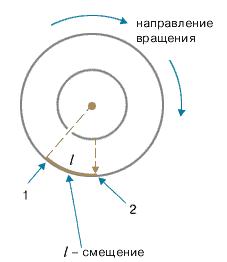
Рис.1.8. 1 – Здесь оседают частицы, когда установка неподвижна. 2 – Здесь оседают частицы при вращении установки.
Зная величины радиусов цилиндров, скорость их вращения и величину смещения легко найти скорость движения атомов (рис. 1.9).
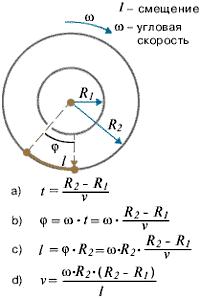 (1.34)
(1.34)
Рис. 1.8.
Время полета атома t от прорези до стенки внешнего цилиндра можно найти, разделив путь, пройденный атомом и равный разности радиусов цилиндров, на скорость атома v. За это время цилиндры повернулись на угол φ, величину которого найдем, умножив угловую скорость ω на время t. Зная величину угла поворота и радиус внешнего цилиндра R2, легко найти величину смещения l и получить выражение, из которого можно выразить скорость движения атома (1.34, d).
При температуре нити 12000С среднее значение скорости атомов серебра, полученное после обработки результатов опытов Штерна, оказалось близким к 600 м/с, что вполне соответствует значению средней квадратичной скорости, вычисленному по формуле (1.28).
1.7.6. Уравнение состояния для газа Ван-дер Вальса.
Уравнение Клапейрона-Менделеева достаточно хорошо описывает газ при высоких температурах и низких давлениях, когда он находится в условиях достаточно далёких от условий конденсации. Однако для реального газа это не всегда выполняется и тогда приходится учитывать потенциальную энергию взаимодействия молекул газа между собой. Простейшим уравнением состояния, описывающим неидеальный газ, является уравнение, предложенное в 1873 г. Иоханнесом Дидериком Ван-дер-Ваальсом (1837 - 1923):
Пусть на молекулы газа действуют силы притяжения и отталкивания. И те, и другие силы действуют на небольших расстояниях, но силы притяжения убывают медленнее сил отталкивания. Силы притяжения относятся к взаимодействию молекулы с её ближайшим окружением, а сила отталкивания - проявляется в момент столкновения двух молекул. Силы притяжения внутри газа в среднем скомпенсированы для каждой отдельной молекулы. На молекулы, расположенные в тонком слое вблизи стенки сосуда, действует сила притяжения со стороны других молекул, направленная внутрь газа, которая создает давление, добавочное к создаваемому самой стенкой. Это давление иногда называют внутренним давлением. Суммарная сила внутреннего давления, действующая на элемент поверхностного слоя газа должна быть пропорциональна числу молекул газа в этом элементе и также числу молекул в слое газа, непосредственно примыкающему к рассматриваемому элементу поверхностного слоя. Толщина этих слоёв определяется радиусом действия сил притяжения и имеет тот же порядок величины. При увеличении концентрации молекул газа в 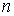 раз, сила притяжения, приходящаяся на единицу площади приповерхностного слоя, возрастёт в
раз, сила притяжения, приходящаяся на единицу площади приповерхностного слоя, возрастёт в 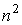 раз. Поэтому величина внутреннего давления растёт пропорционально квадрату концентрации молекул газа. Тогда для суммарного давления внутри газа
раз. Поэтому величина внутреннего давления растёт пропорционально квадрату концентрации молекул газа. Тогда для суммарного давления внутри газа 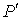 можно записать:
можно записать:
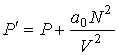 , , | (1.35) |
где: 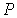 - давление газа, которое действует на стенку сосуда (по третьему закону Ньютона стенка действует на газ с тем же давлением),
- давление газа, которое действует на стенку сосуда (по третьему закону Ньютона стенка действует на газ с тем же давлением), 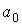 - постоянная, определяемая физико-химическими характеристиками молекул газа,
- постоянная, определяемая физико-химическими характеристиками молекул газа, 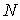 - число молекул газа в объеме
- число молекул газа в объеме 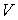 . Отношение
. Отношение 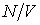 представляет собой концентрацию молекул газа. Вводя обозначение:
представляет собой концентрацию молекул газа. Вводя обозначение:
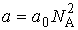 , , | (1.36) |
где: 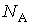 - постоянная Авогадро, имеем
- постоянная Авогадро, имеем
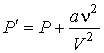 . . | (1.37) |
Итак, нами получен вид поправки к давлению, которая необходима для того, чтобы учесть слабые силы притяжения в реальном газе, отличающие его от идеального. При этом в формуле для нахождения суммарного давления внутри газа 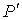 появилась новая постоянная
появилась новая постоянная 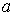 , зависящая от свойств газа.
, зависящая от свойств газа.
Рассмотрим теперь поправку, связанную с действием сил отталкивания. Поскольку нами будут учитываться только парные взаимодействия между молекулами, то эта сила, в отличие от силы притяжения, не будет зависеть от концентрации молекул. По этой же причине сила отталкивания проявляется во всём объёме газа, а не только в приповерхностном слое. Зависимость этой силы от расстояния между молекулами определяет эффективное сечение взаимодействия молекул, то есть, по сути, их размеры.
Таким образом, в случае проявления короткодействующих сил отталкивания, невозможно аппроксимировать молекулы материальными точками и пренебречь их размерами. Поэтому необходимо ввести поправку, учитывающую объём, занимаемый молекулами. Её величина будет пропорциональна общему числу молекул 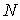 , а также зависеть от их физико-химических свойств. Тогда свободный от молекул объем
, а также зависеть от их физико-химических свойств. Тогда свободный от молекул объем 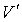 можно определить следующим образом:
можно определить следующим образом:
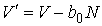 , , | (1.38) |
где: 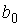 - коэффициент, определяемый свойствами молекул. Вводя обозначение
- коэффициент, определяемый свойствами молекул. Вводя обозначение
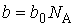 | (1.39) |
представим формулу (1.32) в виде
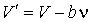 . . | (1.40) |
Величину 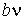 и, таким образом, величину эффективного объёма, занимаемого молекулами, нельзя получить из простых механических моделей, так как сами размеры молекул определяются характером сил отталкивания. Поскольку уравнение Ван-дер-Ваальса является по сути своей эмпирическим, коэффициент
и, таким образом, величину эффективного объёма, занимаемого молекулами, нельзя получить из простых механических моделей, так как сами размеры молекул определяются характером сил отталкивания. Поскольку уравнение Ван-дер-Ваальса является по сути своей эмпирическим, коэффициент 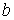 , так же как и коэффициент
, так же как и коэффициент 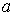 , должны определяться в первую очередь экспериментально.
, должны определяться в первую очередь экспериментально.
Если теперь в левой части уравнения Клапейрона-Менделеева:
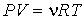 | (1.41) |
произвести замену произведения 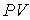 на произведение
на произведение
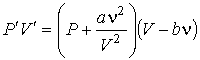 , , | (1.42) |
то получится уравнение Ван-дер-Ваальса
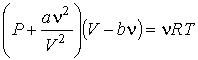 , , | (1.43) |
где: 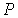 ,
, 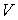 и
и 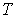 - давление, объём и температура газа,
- давление, объём и температура газа, 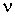 - количество молей газа,
- количество молей газа, 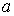 и
и 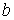 - постоянные для данного газа.
- постоянные для данного газа.
Для различных газов постоянные 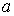 и
и 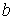 различны, и их можно определить экспериментально. Значение константы
различны, и их можно определить экспериментально. Значение константы 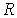 такое же, как и для идеального газа. Введение поправки, обусловленной действием сил притяжения, привело к тому, что уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня. Для уравнения Ван-дер-Ваальса имеют место два следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный. На рис. 1.9 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.
такое же, как и для идеального газа. Введение поправки, обусловленной действием сил притяжения, привело к тому, что уравнение состояния стало кубическим относительно объёма, а число постоянных, являющихся его параметрами, стало равным трем. Как известно, кубическое уравнение имеет три корня. Для уравнения Ван-дер-Ваальса имеют место два следующих случая: а) корни действительны; б) два корня мнимые и один корень действительный. На рис. 1.9 схематически изображены изотермы газа Ван-дер-Ваальса для различных температур.
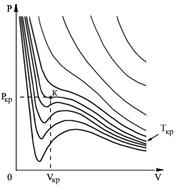
Рис. 1.9. Изотермы газа Ван-дер-Ваальса
На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма 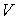 при одинаковых значениях параметров
при одинаковых значениях параметров 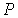 и
и 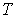 . Это соответствует существованию трёх действительных корней уравнения (1.43). При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 1.9). Эта точка называется критической, а значения
. Это соответствует существованию трёх действительных корней уравнения (1.43). При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 1.9). Эта точка называется критической, а значения 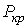 ,
, 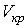 и
и 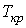 в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения (1.43). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями
в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения (1.43). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями 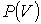 .
.
Критические параметры 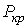 ,
, 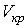 и
и 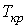 можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба:
можно найти из условия, что в критической точке изотерма Ван-дер-Ваальса имеет как экстремум, так и точку перегиба:
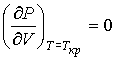 , , | (1.44) |
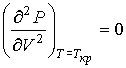 . . | (1.45) |
Решая эти два уравнения совместно с (1.43) можно получить
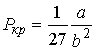 , , | (1.46) |
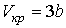 , , | (1.47) |
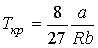 . . | (1.48) |
Таким образом, из уравнения состояния газа Ван-дер-Ваальса следует существование у реальных газов критической точки с параметрами 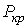 ,
, 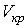 и
и 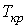 , величина которых зависит от свойств газа.
, величина которых зависит от свойств газа.
Обратимся теперь к экспериментальным обоснованиям уравнения состояния газа Ван-дер-Ваальса. На рис 1.10 показан вид экспериментально полученных изотерм, характерный для многих веществ.
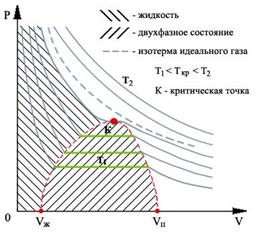 |
| Рис. 1.10. Изотермы реального газа |
На этих кривых виден горизонтальный участок, который заменяет немонотонный участок на изотермах газа Ван-дер-Ваальса. Справа от горизонтального участка экспериментальная изотерма монотонно растет с уменьшением объема, что соответствует сжатию реального газа при постоянной температуре. Горизонтальный участок соответствует сжижению газа, которое при заданной температуре происходит при постоянном давлении. При этом существует двухфазная система жидкость-газ. Наконец, слева от горизонтального участка, где изотерма вновь становится монотонно убывающей функцией 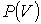 , весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема. Это связано с тем, что размеры молекул жидкостей становятся сравнимы с межмолекулярными расстояниями. Этот участок экспериментальных изотерм наиболее сильно отличается от предсказываемого уравнением для газа Ван-дер-Ваальса.
, весь газ превращается в жидкость. При этом давление очень резко растет с уменьшением объема. Это связано с тем, что размеры молекул жидкостей становятся сравнимы с межмолекулярными расстояниями. Этот участок экспериментальных изотерм наиболее сильно отличается от предсказываемого уравнением для газа Ван-дер-Ваальса.
Экспериментально изотермы могут быть получены при изотермическом сжатии газа в системе, состоящей из сосуда с поршнем, соединенного с манометром. Семейство изотерм для углекислого газа было построено Томасом Эндрюсом (1813 - 1885) во второй половине XIX века. Им было установлено, что при температуре выше 31,1oC углекислота продолжает оставаться газообразной при любом давлении. При более низкой температуре углекислый газ при сильном сжатии переходил в жидкое состояние.
В первой половине XIX века предполагали существование абсолютных газов, которые не могут быть сжижены ни при каких условиях. Однако опыт показал, что любое вещество может быть сжижено при достаточно высоком давлении и низкой температуре.
Совокупность участков изотерм реального газа, соответствующих двухфазным системам жидкость-газ, образуют колоколообразную фигуру (см. рис. 1.10), вершиной которой является критическая точка. При температурах выше критической вещество может существовать только в газообразном состоянии. При температуре ниже критической, вещество может быть сжижено. Критическая температура для гелия очень низкая - 5,2 К. Поэтому долгое время его считали абсолютным газом.
В отличие от гелия, водорода, кислорода и азота, чьи критические температуры достаточно низкие, такие вещества как вода и ртуть (критические температуры 647 К и 1820 К соответственно) существуют как в жидком, так и в газообразном состояниях при комнатных температурах. Поэтому возникли такие термины как "водяной пар" и "пары ртути". Сегодня, с исчезновением понятия "абсолютный газ" исчезло различие понятий "газ" и "пар".
1.8. Явления переноса.
Физическая кинетика изучает процессы, возникающие при нарушениях равновесия. При нарушении равновесия система стремиться вернуться в положение равновесия и, следовательно, это сопровождается ростом энтропии. Таким образом, физическая кинетика изучает необратимые процессы.
Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо электрического заряда и т.п. В связи с этим соответствующие процессы называют явлениями переноса. Каждое явление переноса бывает обусловлено неодинаковостью в пространстве некоторой величины Ω. В случае переноса частиц (диффузии) такой величиной является концентрация частиц – перенос частиц осуществляется в направлении убывания их концентрации. Поток тепла возникает в случае неодинаковости температуры в разных точках среды, причем тепло течет в направлении убывания температуры, и т. д.
При наличии в среде различной концентрации какой-либо примеси возникают диффузионные потоки, то есть явление диффузии. В случае разной температуры - тепловые потоки, то есть явление теплопроводности, при различной скорости течения - потоки импульса или количества движения, то есть явление вязкости.
Термодинамическим потоком 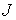 называют количество физической величины, переносимой за одну секунду через выбранную поверхность площадью S. В случае диффузии поток
называют количество физической величины, переносимой за одну секунду через выбранную поверхность площадью S. В случае диффузии поток 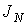 определяет интенсивность переноса частиц примеси. При теплопроводности величина
определяет интенсивность переноса частиц примеси. При теплопроводности величина 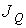 численно равна количеству теплоты, переносимой за единицу времени. Для явления вязкости величина
численно равна количеству теплоты, переносимой за единицу времени. Для явления вязкости величина 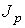 характеризует перенос импульса.
характеризует перенос импульса.
В общем случае поток 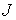 определяется следующим образом:
определяется следующим образом:
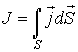 , , | (1.49) |
где: 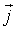 - плотность термодинамического потока, то есть поток, проходящий через единицу площади поверхности,
- плотность термодинамического потока, то есть поток, проходящий через единицу площади поверхности, 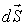 - вектор, численно равный величине элементарной поверхности
- вектор, численно равный величине элементарной поверхности 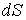 и направленный по нормали к этой поверхности. Если термодинамический поток однороден и вектор
и направленный по нормали к этой поверхности. Если термодинамический поток однороден и вектор 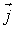 во всех точках среды одинаков и перпендикулярен поверхности, то величина потока
во всех точках среды одинаков и перпендикулярен поверхности, то величина потока 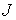 , проходящего через плоскую площадку
, проходящего через плоскую площадку 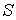 , определяется по формуле:
, определяется по формуле:
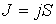 , , | (1.50) |
где 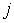 - абсолютное значение (модуль) вектора
- абсолютное значение (модуль) вектора 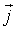 .
.
Опыт показывает, что если рассматриваемая термодинамическая система находится в состоянии, близком к равновесию, то плотность термодинамического потока 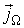 пропорциональна градиенту соответствующей физической величины
пропорциональна градиенту соответствующей физической величины 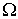 в той же точке:
в той же точке:
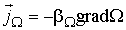 , , | (1.51) |
где 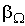 - коэффициенты переноса, или кинетические коэффициенты.
- коэффициенты переноса, или кинетические коэффициенты.
Градиентом называется вектор с компонентами 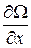 ,
, 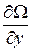 ,
, 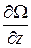 , где Ω – скалярная функция координат x, y, z и обозначается символом grad Ω или
, где Ω – скалярная функция координат x, y, z и обозначается символом grad Ω или 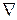 Ω (
Ω (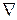 называется математическим оператором набла,
называется математическим оператором набла, 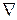 Ω читается градиент Ω).
Ω читается градиент Ω).
Из выражения (6.3) следует, что плотность термодинамического потока 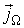 имеет тем большую величину, чем сильнее изменяется физическая величина
имеет тем большую величину, чем сильнее изменяется физическая величина 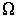 от точки к точке пространства. Кроме этого, знак минус в этом выражении указывает на то, что поток
от точки к точке пространства. Кроме этого, знак минус в этом выражении указывает на то, что поток 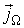 направлен в сторону уменьшения величины
направлен в сторону уменьшения величины 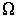 .
.
Величина 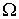 зависит от описываемого процесса. При описании диффузии в качестве параметра
зависит от описываемого процесса. При описании диффузии в качестве параметра 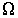 выступает относительная концентрация примеси. Коэффициент переноса
выступает относительная концентрация примеси. Коэффициент переноса  представляет собой коэффициент диффузии
представляет собой коэффициент диффузии 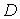 . Для случая теплопроводности вместо
. Для случая теплопроводности вместо 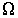 необходимо использовать энергию теплового движения молекулы. Коэффициент
необходимо использовать энергию теплового движения молекулы. Коэффициент  является коэффициентом теплопроводности κ. Параметром
является коэффициентом теплопроводности κ. Параметром 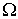 при описании вязкости будет импульс упорядоченного движения молекулы, а величина
при описании вязкости будет импульс упорядоченного движения молекулы, а величина  - это коэффициент вязкости η.
- это коэффициент вязкости η.
В случае если величина 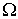 зависит только от одной пространственной переменной (одномерная среда), формула для плотности потока (6.3) приобретает более простой вид:
зависит только от одной пространственной переменной (одномерная среда), формула для плотности потока (6.3) приобретает более простой вид:
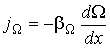 | (1.53) |
или для потока 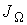 :
:
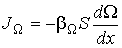 . . | (1.54) |
1.8.1. Эффективный диаметр молекулы.
Эффективный диаметр молекулы – расстояние d, на которое сближаются центры двух молекул при столкновении. Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами (рис. 1.11). Здесь σ – площадь, в которую не может проникнуть центр любой другой молекулы. Здесь 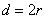 – диаметр молекулы. Площадь, ограниченную штриховой окружностью на рис. 1.12, называют эффективным сечением молекулы:
– диаметр молекулы. Площадь, ограниченную штриховой окружностью на рис. 1.12, называют эффективным сечением молекулы:
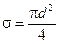 (1.55)
(1.55)
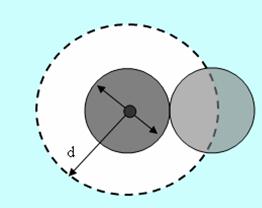
Рис. 1.11.
1.8.2. Средняя длина пробега молекул.
Средней длиной свободного пробега называется расстояние, проходимое молекулой в среднем без столкновений. Средняя длина свободного пробега равна:
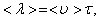 (1.56)
(1.56)
где 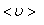 – средняя скорость теплового движения, τ – среднее время между двумя столкновениями. Именно
– средняя скорость теплового движения, τ – среднее время между двумя столкновениями. Именно 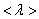 - средняя длина свободного пробега нас интересует (рис. 1.13)
- средняя длина свободного пробега нас интересует (рис. 1.13)
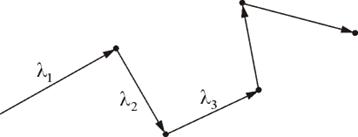
Рис. 1.12.
Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», - при относительно высокой скорости теплового движения молекул (103 м/с) объясняется столкновениями молекул. Молекула газа время от времени сталкивается с другими молекулами. В момент столкновения молекула резко изменяет величину и направление скорости своего движения.
Модель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении.
За одну секунду молекула проходит путь, равный средней арифметической скорости 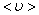 . За ту же секунду молекула претерпевает ν столкновений. Следовательно,
. За ту же секунду молекула претерпевает ν столкновений. Следовательно,
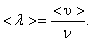 (1.57)
(1.57)
Подсчитаем число столкновений. Вероятность столкновения трех и более молекул бесконечно мала. Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рис. 1.13).
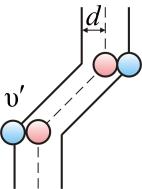
Рис. 1.13.
Путь, который пройдет молекула за одну секунду, равен длине цилиндра 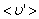 . Умножим объём цилиндра
. Умножим объём цилиндра 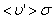 на число молекул в единице объёма n, получим среднее число столкновений в одну секунду:
на число молекул в единице объёма n, получим среднее число столкновений в одну секунду:
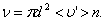 (1.58)
(1.58)
На самом деле, все молекулы движутся (и в сторону, и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга. По закону сложения случайных величин
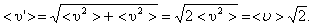 (1.59)
(1.59)
А так как средняя длина свободного пробега 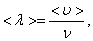 то получим:
то получим:
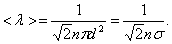 (1.60)
(1.60)
Уравнение состояния идеального газа позволяет нам выразить n через давление P и термодинамическую температуру Т.
Так как 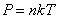 , то есть
, то есть 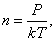 то
то 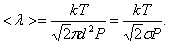
Таким образом, при заданной температуре средняя длина свободного пробега обратно пропорциональна давлению Р:
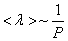 . (1.61)
. (1.61)
Например, при d = 3 Å = 3×10-10 м, Р = 1 атм., Т = 300 К, 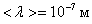 а, т.к.
а, т.к. 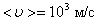 , то
, то 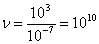 столкновений.
столкновений.
1.8.3. Диффузия.
Диффузией называется процесс самопроизвольного выравнивания концентраций веществ в смесях. Она наблюдается в различных средах, но её скорость сильно зависит от агрегатного состояния вещества. В газах это явление происходит достаточно быстро, что мы можем, в частности, наблюдать по тому, как происходит распространение запахов в воздухе. В жидкостях явление диффузии происходит значительно медленнее и проявляется, например, при растворении в них твердых тел или при взаимном смешивании различных жидкостей. Для наблюдения диффузии в твердых телах обычно требуется очень большое время.
Опытным путем установлено, что поток молекул i -того вида через перпендикулярную к оси x поверхность S определяется выражением
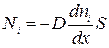 , (1.62)
, (1.62)
где D – коэффициент диффузии, измеряемый в м2/с.
Умножим обе части (1.62) на массу молекулы i -того вида mi. Получим выражение для потока массы i -той компоненты:
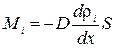 . (1.63)
. (1.63)
Здесь ρ i = nimi – парциальная плотность i -той компоненты; ее называют также абсолютной концентрацией.
Формулы (1.62) и (1.62) представляют собой эмпирические уравнения диффузии. Их называют также законом Фика.
1.5.4. Теплопроводность.
Теплопроводность - это явление, приводящее к выравниванию температуры в различных точках среды. Опыт дает, что если в некоторой среде (твердой, жидкой или газообразной) создать вдоль оси x перепад температуры, проекция которого на ось x называется градиентом и может быть выражена как производная от температуры по координате 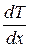 , то поток тепла q через поверхность S, расположенную перпендикулярно к оси x выражается формулой:
, то поток тепла q через поверхность S, расположенную перпендикулярно к оси x выражается формулой:
 . (1.64)
. (1.64)
Знак минус в формуле (1.64) отражает то обстоятельство, что тепло течет в направлении убывания температуры. Поэтому знаки q и 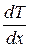 противоположны. Коэффициент пропорциональности κ называется коэффициентом теплопроводности. Коэффициент теплопроводности измеряется в Вт/(м∙К), является табличной величиной и зависит от свойств среды. Наибольшую теплопроводность имеют металлы, а наименьшую - различные теплоизоляционные материалы, такие как асбест, пенопласт и т.д. Достаточно большая теплопроводность металлов связана с тем, что в них перенос теплоты осуществляется не вследствие хаотического движения атомов и молекул, как, например, в газах или жидкостях, а свободными электронами, имеющими гораздо большие скорости теплового движения.
противоположны. Коэффициент пропорциональности κ называется коэффициентом теплопроводности. Коэффициент теплопроводности измеряется в Вт/(м∙К), является табличной величиной и зависит от свойств среды. Наибольшую теплопроводность имеют металлы, а наименьшую - различные теплоизоляционные материалы, такие как асбест, пенопласт и т.д. Достаточно большая теплопроводность металлов связана с тем, что в них перенос теплоты осуществляется не вследствие хаотического движения атомов и молекул, как, например, в газах или жидкостях, а свободными электронами, имеющими гораздо большие скорости теплового движения.
1.8.5.Вязкость или внутреннее трение
Явление вязкости или внутреннего трения наблюдается как в газах и жидкостях, так и в твердых телах. Оно приводит к возникновению силы сопротивления при движении тела в жидкости или газе, и к затуханию звуковых волн при прохождении их через различные среды. В частности, с явлением вязкого трения связан процесс затухания колебаний в механических осцилляторах.
При изучении течения Куэтта вязкой жидкости (или газа), зажатой между двумя пластинами, находящимися на расстоянии h друг от друга, при чем одна из пластин двигалась со скоростью V, экспериментально была получена формула для силы сопротивления
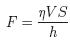 , (1.65)
, (1.65)
где отношение 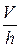 , в сущности, представляет собой проекцию градиента скорости на ось координат, перпендикулярную к потоку, то есть может быть представлена в виде производной от скорости по соответствующей координате. Тогда сила трения между двумя слоями жидкости или газа равна:
, в сущности, представляет собой проекцию градиента скорости на ось координат, перпендикулярную к потоку, то есть может быть представлена в виде производной от скорости по соответствующей координате. Тогда сила трения между двумя слоями жидкости или газа равна:
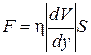 , (1.66)
, (1.66)
где η – коэффициент вязкости. Уравнение (1.66) есть эмпирическое уравнение вязкости.
Согласно второму закону Ньютона взаимодействие двух слоев с силой F можно рассматривать как процесс, в ходе которого от одного слоя к другому происходит изменение импульса в единицу времени, которое по величие равно силе F. Поэтому уравнение (1.66) можно представить в виде
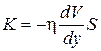 (1.67)
(1.67)
где K – импульс, передаваемый за секунду от слоя к слою через поверхность S, то есть поток импульса через S. Поток импульса измеряется в кгм/с2. Следовательно, единицей коэффициента вязкости η является кг/(м∙с), которую можно представить также в виде Па∙с.
Знак минус в формуле (1.67) обусловлен тем обстоятельством, что импульс «течет» в направлении убывания скорости. Поэтому знаки потока импульса K и производной dV/dy противоположны.
Напомним, что формула (1.66) определяет одинаковый модуль двух противоположно направленных сил, с которыми слои действуют друг на друга. Поэтому в формуле (1.66) нельзя ставить перед правой частью знак минус. Кроме того, нужно брать модуль выражения dV/dy (модуль силы при любом знаке производной dV/dy должен быть положительным).
С точки зрения молекулярно-кинетической теории основной причиной переноса в средах является тепловое хаотическое движение их микрочастиц. Находясь в постоянном хаотическом движении, молекулы газа, соударяясь между собой, передают друг другу свою кинетическую энергию. Это приводит к выравниванию температуры в различных частях газа. Аналогично при тепловом движении происходит выравнивание концентраций веществ в смеси и передача импульса между движущимися друг относительно друга слоями жидкости.
При описании термодинамических потоков будем предполагать, что в среде не происходит процесса макроскопического перемешивания, и перенос осуществляется только из-за неупорядоченного движения микрочастиц среды. Однако в реальном газе и жидкости может возникнуть перемешивание, как вследствие каких-либо механических воздействий, так и при конвекции.
Явление конвекции возникает в жидкостях и газах благодаря полю силы тяжести. Оно имеют место, в частности, если нагрев жидкости происходит снизу, а её охлаждение сверху. Нижние слои при этом расширяются, и начинается подъём более нагретой жидкости. При этом перенос теплоты будет происходить за счет макроскопического движения среды. Аналогичный процесс наблюдается и при смешивании двух жидкостей, если более плотную жидкость налить сверху на менее плотную, например воду на глицерин или спирт.
1.8.6. Описание явлений переноса в газах
Процессы переноса в газах могут быть описаны с использованием молекулярно-кинетической теории. Такое описание дает правильные выражения для уравнений переноса и приближенные (с точность до постоянного множителя порядка единицы) формулы для расчета коэффициентов переноса. Полученные значения для коэффициентов переноса оказываются несколько заниженными по сравнению с их выражениями, получаемыми при точных расчетах, которые обычно проводятся с использованием методов статистической физики.
Будем считать, что молекулы газа совершают хаотическое тепловое движение. В этом случае можно предположить, что вероятность движения молекулы в любом направлении одинакова. Так как таких возможных направлений движения всего шесть, соответствующих движению в положительном и отрицательном направлении вдоль осей 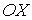 ,
, 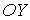 и
и 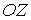 , то плотность потока частиц
, то плотность потока частиц 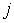 в любом из этих направлений может быть определена по формуле:
в любом из этих направлений может быть определена по формуле:
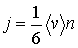 (1.68)
(1.68)
где: 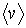 - средняя скорость теплового движения молекул,
- средняя скорость теплового движения молекул, 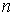 - концентрация молекул газа.
- концентрация молекул газа.
На рис. 1.14 схематически изображен процесс переноса некоторой физической величины 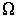 через площадку
через площадку 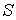 . Будем считать, что величина
. Будем считать, что величина 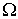 изменяется в зависимости от координаты
изменяется в зависимости от координаты 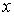 . В качестве переносимой величины может выступать масса, энергия, импульс и т.д. При этом считаем, что переносимую величину можно отнести к одной молекуле. Если речь идет, например, о переносе энергии, то отнесенной к одной молекуле величиной будет полная энергия молекулы.
. В качестве переносимой величины может выступать масса, энергия, импульс и т.д. При этом считаем, что переносимую величину можно отнести к одной молекуле. Если речь идет, например, о переносе энергии, то отнесенной к одной молекуле величиной будет полная энергия молекулы.
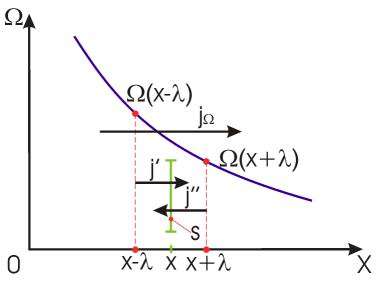
Рис. 1.14. Схема к выводу уравнения переноса
Через площадку  в направлении оси
в направлении оси  будет проходить поток молекул
будет проходить поток молекул  , а в противоположном направлении соответственно поток
, а в противоположном направлении соответственно поток 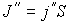 . В случае выполнения принципа детального равновесия, плотности потоков молекул в двух противоположных направлениях должны быть одинаковыми:
. В случае выполнения принципа детального равновесия, плотности потоков молекул в двух противоположных направлениях должны быть одинаковыми: 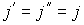 или
или 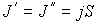 . Переносимый в направлении оси
. Переносимый в направлении оси 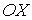 поток величины
поток величины 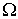 отличается от потока этой величины, переносимого в обратном направлении. Это связано с тем, что в рассматриваемом газе через площадку
отличается от потока этой величины, переносимого в обратном направлении. Это связано с тем, что в рассматриваемом газе через площадку 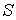 в направлении оси
в направлении оси 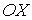 будут проходить молекулы, характеризуемые величиной
будут проходить молекулы, характеризуемые величиной 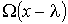 , а в противоположном - соответственно величиной
, а в противоположном - соответственно величиной 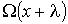 , где
, где 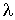 - длина свободного пробега молекул газа, численно равная перемещению, которое молекула газа проходит без соударения с другими молекулами. Тогда плотность потока величины
- длина свободного пробега молекул газа, численно равная перемещению, которое молекула газа проходит без соударения с другими молекулами. Тогда плотность потока величины 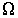 с учетом выражения (6.6) можно вычислить по формуле:
с учетом выражения (6.6) можно вычислить по формуле:
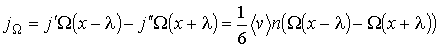 (1.69)
(1.69)
Считая длину свободного пробега 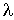 малой величиной, функцию
малой величиной, функцию 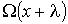 (и соответственно функцию
(и соответственно функцию 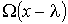 ) можно разложить в ряд с сохранением только слагаемого первого порядка малости:
) можно разложить в ряд с сохранением только слагаемого первого порядка малости:
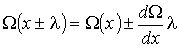 (1.70)
(1.70)
Тогда разность значений 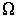 в формуле (1.70) принимает вид:
в формуле (1.70) принимает вид:
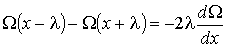 (1.71)
(1.71)
Окончательно получаем уравнение переноса для плотности потока физической величины 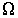 :
:
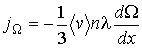 (1.72)
(1.72)
а соответственно для потока 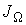 имеем:
имеем:
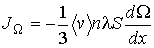 (1.73)
(1.73)
Стоящие в полученных выражениях (1.72) и (1.73) величины средней скорости 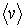 , концентрации молекул
, концентрации молекул 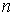 и переносимой физической величины
и переносимой физической величины 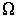 зависят только от координаты
зависят только от координаты 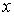 и принимают значения, соответствующие точке с координатой
и принимают значения, соответствующие точке с координатой 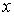 .
.
Полученное уравнение переноса применимо для описания явлений диффузии, теплопроводности и вязкости в газах при отсутствии в них макроскопического перемешивания.
Проведем описание диффузии примеси одного газа в другом. Для простоты будем считать, что оба газа имеют практически одинаковые молекулы и их суммарная концентрация постоянна и равна величине 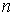 :
: 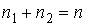 , где
, где 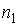 и
и 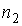 - концентрации газов. Введение последнего условия необходимо для того, чтобы в системе не возникало макроскопическое перемешивание газов, а их взаимное проникновение происходило только за счет диффузии.
- концентрации газов. Введение последнего условия необходимо для того, чтобы в системе не возникало макроскопическое перемешивание газов, а их взаимное проникновение происходило только за счет диффузии.
Пусть концентрация диффундирующего газа 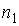 зависит только от одной координаты
зависит только от одной координаты 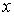 :
: 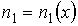 . Тогда физической величиной, перенос которой в данном случае осуществляется вследствие диффузии, является относительная концентрация газа, которая также зависит только от переменной
. Тогда физической величиной, перенос которой в данном случае осуществляется вследствие диффузии, является относительная концентрация газа, которая также зависит только от переменной 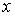 :
:
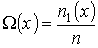 (1.74)
(1.74)
Подстановка этого выражения в формулу (1.73) дает уравнение диффузии в виде:
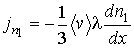 (1.75)
(1.75)
Соответственно выражение для потока частиц 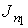 принимает форму:
принимает форму:
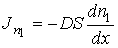 (1.76)
(1.76)
где введенный коэффициент 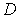 называется коэффициентом диффузии:
называется коэффициентом диффузии:
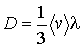 (1.77)
(1.77)
Выражения, аналогичные формулам (1.76) и (1.77), могут быть записаны и для второго газа, имеющего концентрацию 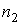 .
.
Уравнение (1.76) позволяет также записать формулу, описывающую поток массы. Считая, что молекула газа имеет массу 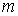 , умножим на эту величину уравнение (1.77) и учтем связь величины потока массы
, умножим на эту величину уравнение (1.77) и учтем связь величины потока массы 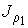 и потока концентрации частиц
и потока концентрации частиц 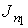 :
:
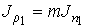 .
.
Тогда имеем:
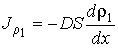 (1.78)
(1.78)
где: 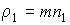 - плотность диффундирующего газа.
- плотность диффундирующего газа.
С учетом формулы для длины свободного пробега (1.60)
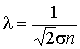 ,
,
где 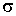 – эффективное сечение молекулы газа, и выражения (1.31) для средней скорости:
– эффективное сечение молекулы газа, и выражения (1.31) для средней скорости: 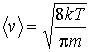 ,
,
выражение для коэффициента диффузии приобретает вид:
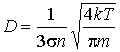 (1.79)
(1.79)
Как следует из этой формулы, коэффициент диффузии растет с повышением температуры: 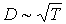 и уменьшается при увеличении концентрации:
и уменьшается при увеличении концентрации: 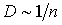 . Уменьшение коэффициента диффузии при увеличении концентрации молекул связано с уменьшением длины свободного пробега
. Уменьшение коэффициента диффузии при увеличении концентрации молекул связано с уменьшением длины свободного пробега 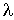 , что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
, что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
При описании теплопроводности в качестве переносимой величины 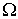 выступает энергия теплового движения молекулы газа:
выступает энергия теплового движения молекулы газа:
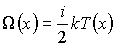 (1.80)
(1.80)
где: 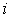 - число степеней свободы молекулы, а температура считается зависящей только от координаты
- число степеней свободы молекулы, а температура считается зависящей только от координаты 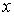 :
: 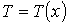 . Тогда подстановка формулы (1.80) в выражение (1.70) дает уравнение теплопроводности:
. Тогда подстановка формулы (1.80) в выражение (1.70) дает уравнение теплопроводности:
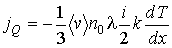 (1.81)
(1.81)
Если учесть соотношение
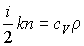 (1.82)
(1.82)
где: 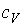 - удельная теплоемкость газа при постоянном объеме,
- удельная теплоемкость газа при постоянном объеме, 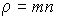 - плотность газа, то уравнение (1.81) приобретет форму
- плотность газа, то уравнение (1.81) приобретет форму
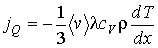 , (1.83)
, (1.83)
а выражение для потока теплоты 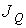 через площадку площадью
через площадку площадью 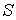 , перпендикулярную оси
, перпендикулярную оси 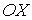 , соответственно запишется в виде:
, соответственно запишется в виде:
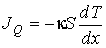 (1.84)
(1.84)
В формуле (1.84) введен коэффициент теплопроводности, который равен:
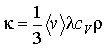 (1.85)
(1.85)
При подстановке в эту формулу выражений для длины свободного пробега (1.60) и средней скорости (1.31) имеем:
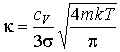 (1.86)
(1.86)
Из этой формулы следует, что с повышением температуры, коэффициент теплопроводности тоже увеличивается: 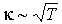 . Но в отличие от коэффициента диффузии, этот коэффициент не зависит от концентрации молекул газа.
. Но в отличие от коэффициента диффузии, этот коэффициент не зависит от концентрации молекул газа.
Эта особенность связана с тем, что в более плотном газе в теплопроводности участвует большее количество молекул. Но при этом, вследствие меньшей длины свободного пробега 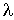 , энергия передается на меньшие расстояния. Для более разреженного газа ситуация обратная: в переносе энергии участвует меньшее число молекул, но этот перенос осуществляется на большие расстояния.
, энергия передается на меньшие расстояния. Для более разреженного газа ситуация обратная: в переносе энергии участвует меньшее число молекул, но этот перенос осуществляется на большие расстояния.
Отметим так же, что независимость теплопроводности от концентрации молекул газа справедлива только в том случае, если в нем отсутствует макроскопическое перемешивание, и перенос энергии осуществляется без переноса вещества.
Явление вязкости газа может быть описано с помощью уравнения (1.71) при подстановке в него в качестве переносимой величины 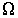 импульса молекулы при упорядоченном движении газа в направлении, перпендикулярном оси
импульса молекулы при упорядоченном движении газа в направлении, перпендикулярном оси 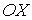 :
:
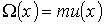 (1.87)
(1.87)
где: 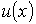 - скорость течения газа в направлении, перпендикулярном оси
- скорость течения газа в направлении, перпендикулярном оси 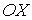 , в точке с координатой
, в точке с координатой 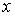 :
: 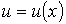 . С учетом формулы (1.72) получим уравнение вязкости в виде:
. С учетом формулы (1.72) получим уравнение вязкости в виде:
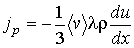 (1.88)
(1.88)
Тогда формула для расчета потока импульса 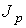 приобретет вид
приобретет вид
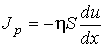 (1.89)
(1.89)
где коэффициент вязкости 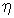 определяется с помощью следующего выражения
определяется с помощью следующего выражения
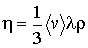 (1.90)
(1.90)
Величина 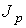 имеет смысл силы, с которой слои газа, двигающиеся в направлении, перпендикулярном оси
имеет смысл силы, с которой слои газа, двигающиеся в направлении, перпендикулярном оси 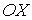 , действуют друг на друга.
, действуют друг на друга.
После подстановке в формулу (1.90) выражений (1.60) и (1.31) имеем:
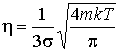 (1.91)
(1.91)
Температурная зависимость коэффициента вязкости аналогична зависимости для коэффициента теплопроводности: 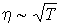 , и этот коэффициент, также как и теплопроводность, не зависит от концентрации молекул газа (плотности газа).
, и этот коэффициент, также как и теплопроводность, не зависит от концентрации молекул газа (плотности газа).
Независимость коэффициента вязкости от плотности газа имеет то же объяснение, что и для теплопроводности. С повышением плотности увеличивается число молекул, переносящих импульс, но уменьшаются расстояния, на которые этот перенос осуществляется.
Как было отмечено выше, коэффициенты диффузии 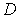 , теплопроводности
, теплопроводности 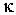 и вязкости
и вязкости 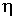 возрастают с увеличением температуры, пропорционально
возрастают с увеличением температуры, пропорционально 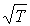 . Указанная зависимость связана с возрастанием пропорционально
. Указанная зависимость связана с возрастанием пропорционально 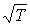 средней скорости движения молекул газа (см. формулу (1.31). Но, как показывают экспериментальные исследования, эти коэффициенты с повышением температуры растут несколько быстрее, чем
средней скорости движения молекул газа (см. формулу (1.31). Но, как показывают экспериментальные исследования, эти коэффициенты с повышением температуры растут несколько быстрее, чем 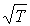 . Это связано с тем, что с увеличением температуры происходит некоторое уменьшение эффективного сечения молекул газа
. Это связано с тем, что с увеличением температуры происходит некоторое уменьшение эффективного сечения молекул газа 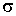 , а величина
, а величина 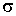 стоит в знаменателях формул для коэффициентов диффузии (1.79), теплопроводности (1.86) и вязкости (1.91).
стоит в знаменателях формул для коэффициентов диффузии (1.79), теплопроводности (1.86) и вязкости (1.91).
Между всеми полученными коэффициентами переноса существует общее соотношение, имеющее следующий вид:
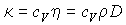 , (1.92)
, (1.92)
которое позволяет по результатам измерений одного из коэффициентов переноса вычислять все остальные.
Кроме этого, полученные соотношения дают возможность по экспериментально измеренным коэффициентам диффузии, теплопроводности или вязкости определять длину свободного пробега молекулы газа и её эффективное сечение. Это, в свою очередь, позволяет находить диаметр молекулы.
В заключение отметим еще раз, что полученные выражения для коэффициентов переноса являются приближенными с точностью до некоторого безразмерного множителя порядка единицы.
Задача 1.5.1. Определить зависимость от температуры коэффициентов диффузии, теплопроводности и вязкости для газа, находящегося при постоянном давлении.
Решение: Будем считать, что уравнение состояния газа имеет вид:
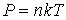
Тогда выразив из этой формулы концентрацию газа 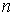 и подставив в выражение (1.96), получим формулу для коэффициента диффузии:
и подставив в выражение (1.96), получим формулу для коэффициента диффузии:
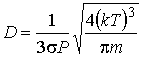
Как следует из этой формулы, при указанном процессе коэффициент диффузии пропорционален температуре в степени 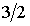 :
: 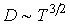 .
.
Так как коэффициенты теплопроводности и вязкости не зависят от концентрации молекул газа, и, следовательно, от изменения его давления, то для определения их температурной зависимости можно использовать формулы (1.86) и (1.91) соответственно.
 2015-04-01
2015-04-01 22694
22694
