Статистические игры

Во многих практических ситуациях приходится рассчитывать случаи, когда один из игроков нейтрален, т.е. не стремится извлечь max выгоду или обратить в свою пользу ошибки противника. К таким играм относят ситуации в которых в качестве одного из игроков выступает природа (вся совокупность внешних обстоятельств, которые не имеют злого умысла, а развиваются и действуют по своим законам).

У человека есть возможность, наблюдая сложившиеся обстоятельства изучать противника посредством проведения эксперимента. Если этот эксперимент не ограничен, то знания можно сделать сколь угодно полными и принимать решения в условиях неопределенности, однако это может быть невозможно в силу обстоятельств. Проведение эксперимента требует больших затрат времени, затраты средств могут быть больше чем выгода от добавочных знаний, поэтому возникает необходимость принять решение о целесообразности проведения эксперимента и если эксперимент проводится, то необходимо принять решение об его завершении и действиях после его окончания. Игры, в которых один игрок природа другой человек называются статистическими. Стратегии природы это полная совокупность внешних условий, в которых приходится принимать решения, называются состояниями природы.

Пространство состояний 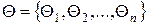. Множество A={a₁, a₁, …, a_k,}- пространство частых стратегий статистика. a_i – возможные действия статистика. Оценка действий статистика определяется функцией потерь для всех возможных комбинаций элементов множества 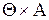. Оценка может быть задана аналитически или при помощи матрицы потерь .

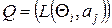Знание априорного распределения вероятности позволяет определить средние потери, которые несет статистик, выполняя свои действия.

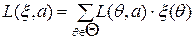
Наилучшим для статистика считается байесовское действие a­^*­, которое обеспечивает min потери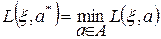

Кроме чистых стратегий у статистика бывают смешанные 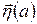стратегии, задаваемые распределением вероятностей, которые определены как вероятности использования чистых стратегий a₁, a₂,... a_k для статистика.

Множество H={η(a₁), η(a₂), …, η(a_k)} – пространство смешанных стратегий статистика. Смешанные стратегии статистика и природы обуславливают средние потери статистика. .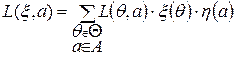

При этом задача статистика состоит в выборе такой стратегии η^*(a) при которой средние потери будут минимальны. .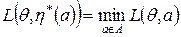

Пример: Задача о замене оборудования.

Установленное на предприятии оборудование может оказаться в одном из 3 состояний: θ₁ – оборудование работоспособно и требует небольшого текущего ремонта.

θ₂ – некоторые детали требуют большого ремонта или замены.

θ₃ – основные детали износились на столько, что дальнейшая эксплуатация оборудования невозможна.

Для предприятия возможны 3 способа действия:

а₁ – оставить оборудование еще на 1 год проведя ремонт своими силами.

а₂ – провести капитальный ремонт с вызовом специальной бригады ремонтников.

а₃ – замена оборудования новым.

Потери предприятия, при различных способах действия включая стоимость ремонта, замены оборудования убытки, связанные с ухудшением качества продукции с простоями вызванными неисправностью оборудования указаны в таблице. Из опыта работы предприятия известно, что состояние θ_i встречается соответственно в 20%, 50%, 30% случаев.

L(θi,a)	a1	a2	a3
θ1
θ2
θ3

Тогда, применяя байесовский подход, вычислим средние потери, чтобы определить оптимальную чистую стратегию статистика.

L₁ =0,2*1+0,5*5+0,3*7=4,8

L₂=0,2*3+0,5*2+0,3*7=3,4=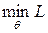

L₃=0,2*5+0,5*4+0,3*3=3,9

а₂=а^*

Статистическая игра может быть представлена в виде обычной игры(S – игры) заданной множеством точек C₁, C₁, …, C_n в m мерном пространстве. Координатами этих точек являются потери статистика(2-го игрока), при всевозможных чистых стратегиях 1-го игрока.

Не существует универсального правила позволяющего выбрать определенный образ действий независимо от сложившейся ситуации. При рассмотрении смешанной стратегии статистика η(а) можно лишь указать следующие характерные ситуации:

1. Нельзя найти ни одной стратегии лучшей стратегии η(а), т.е

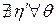
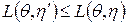η(а) – допустимая стратегия.

2. Если η(а) недопустимая стратегия, то 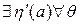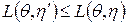, тогда стратегия η(а) исключается в пользу стратегии η^/(а).

Например, для двумерного пространства, когда множество стратегий описывается областью S, мы находим самую левую, самую нижнюю точку.

AB – допустимое множество стратегий статистика.

A

B

3. Принципом выбора называется правило позволяющее определить наилучшую смешанную стратегию статистика. Выделяют следующие принципы выбора:

1) Принцип минимакса. Выбор стратегии η^* обеспечивает минимальные потери при наихудшем состоянии природы.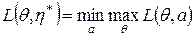

Этот принцип исходит из предположения, что природа действует наихудшим для статистика образом. Является оправданным в стратегических играх, но в статистических играх выражает точку зрения крайнего пессимизма и не учитывает априорную информацию о состоянии природы, поэтому рекомендован в тех случаях, когда отсутствует априорная информация или есть основания сомневаться в ее достоверности.

2) Принцип минимакса дополнительных потерь. Выбор стратегии η^* осуществляется исходя из дополнительных потерь.

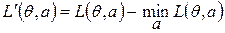
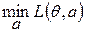- это минимальные потери, которые статистик несет обязательно, даже при своем наилучшем действии, т.е необходимые потери, которые могут быть компенсированы каким-то образом и могут не учитываться при выборе стратегии

3) Байесовский принцип. Учитывает априорные распределения вероятностей 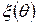и смешанная стратегия статистика оценивается путем усреднения потерь по всем возможным состояниям природы 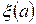, тогда Байесовская стратегия:

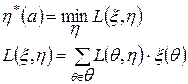
Статистические игры позволяют уточнить состояние природы путем постановки эксперимента, однако это требует затрат средств и времени.

Единичным экспериментом называется эксперимент с заранее определенным объемом и порядком проведения серии испытаний. Пусть Z – пространство исходов Z_i, проводимого эксперимента. исходы эксперимента связанны с состоянием природы условными вероятностями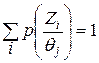

Пространство выбора – это множество 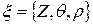задается при помощи таблицы содержащей распределение вероятностей 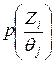на множестве 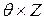. Статистик принимает решение в зависимости от исхода эксперимента Z_i. Правила d(Z), определяющие решение 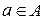, которое должен принять статистик при исходе Z называются решающей функцией.

Любую решающую функцию можно рассматривать как разбиение пространства Z на классы. Если статистик выбрал некоторую функцию d(z) в чем и состоит решение задачи, то ему соответствуют потери. Поэтому для оценки решающей функции используется функция риска, соответствующая всевозможным исходам эксперимента.

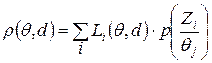
Пространство решающих функций это пространство содержащее полный перечень решающих функций и из него происходит выбор в игре и единичном эксперименте. При использовании смешанных стратегий должен существовать механизм случайного выбора, задающий распределение вероятностей η(d) и функция риска примет вид:

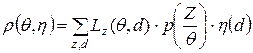
Принцип минимакса состоит в том, чтобы выбрать стратегию η(d) при которой средний риск, при наихудшем для статистика состоянии природы, был минимальным, т.е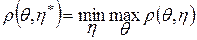

Ожидаемый риск – это средний риск с учетом всех возможных состояний природы и априорного распределения вероятностей на пространстве θ. Для Байесовского принципа статистик может ограничится использованием только чистых, поэтому ожидаемый риск: 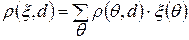, а байесовский принцип требует такого применения решающей функции d^*, при которой ожидаемый риск будет минимальным т.е .

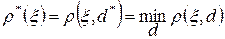Пусть N – общее число чистых стратегий статистика в игре с единичным экспериментом. Если l это число возможных действий статистика в игре без эксперимента, ν - число возможных исходов, то N= l ^ν. При применении Байесовского подхода к определению оптимальной стратегии вместо априорного распределения вероятностей следует использовать апостериорное с целью упрощения решения. Дело в том, что априорное распределение вероятностей 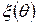дает информацию о том насколько часто то или иное состояние природы встречается вообще, безотносительно к тем конкретным условиям, в которых статистику приходится принимать решение. Целью эксперимента является получение дополнительной информации о действительном состоянии природы, и вместо априорного получается апостериорное распределение на пространстве θ при данном конкретном исходе эксперимента. Это распределение получается по формуле Байеса:

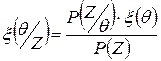, где ;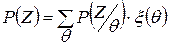

Знание апостериорного распределения позволяет оценивать состояние природы, используя принцип максимального правдоподобия, согласно которому за оценку состояния природы принимают то состояние, которое наиболее вероятно на основании опытных данных.

Проблема необходимости рассмотрения большого количества исходов эксперимента снимается рассмотрением задачи для какого-нибудь конкретного случая, при помощи апостериорного распределения вероятности. В этом случае в качестве чистых стратегий статистика используются элементы пространства решений A. При этом каждому решению 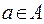будут соответствовать потери.

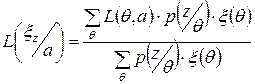
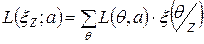- безусловные потери.

Байесовский принцип сводится к тому, чтобы выбрать такое действие a^* при котором величина потерь будет минимальна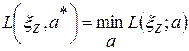

Пример. Задача о технологической линии.

На линию может поступать сырье с малым количеством примесей ситуация θ₁, с большим количеством примесей θ₂.

Предусмотрены 3 режима работы а₁, а₂, а₃. Потери, отражающие качество выпускаемой продукции и расходы сырья в зависимости от качества сырья и режима работы представлены в таблице.

	а1	а2	а3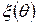
θ1				0,6
θ2				0,4

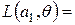0*0,6+5*0,4=2

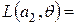1*0,6+3*0,4=1,8=min L

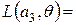3*0,6+2*0,4=2,6

Определив апостериорное распределение вероятностей по известным априорным распределениям и условным распределениям P(Z/θ).

	априорное распределение	P(Z/θ)		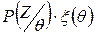Апостериорное распределение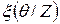
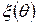	Z1	Z2	Z3	Z1	Z2	Z3	Z1	Z2	Z3
θ1	0,6	0,6	0,25	0,15	0,36	0,15	0,09	0,818	0,355	0,31
θ2	0,4	0,2	0,3	0,5	0,08	0,12	0,2	0,182	0,445	0,69
P(Z)					0,44	0,27	0,29

Согласно принципу максимального правдоподобия θ=θ₁ это то состояние, которое принимает природа, и поэтому принимаем решение о наладке линии в соответствии с этим состоянием.

Пример. Задача о радиолокационной станции (РЛС).

Сигнал может появлятся или при наличии цели в зоне досягаемости или в результате действия различных помех. Тогда могут быть 2 состояния природы:

θ₁ – цель есть, θ₂ – цели нет. Можно принять 2 решения а₁ – пуск, а₂ – нет. Могут быть допущены ошибки 2 видов а₁/θ₂ – ошибка 1-го рода (ложная тревога), а₂/θ₁ – ошибка 2-го рода (пропуск цели).

Для принятия решения в двухальтернативной задаче используют отношение правдоподобия, определяемое соотношением:

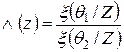
Если заданно число К, по значению которого принимают решение, по одному из этих правил:

решение а₁ если 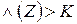, а₂ если 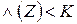, а₁ или а₂ если .

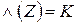Значение К выбирают в зависимости от последствий, к которым может привести ошибочное решение. Так в данной задаче ошибка «ложная тревога» может иметь большие последствия чем «пропуск цели», поэтому решение а₁ следует принимать если цель действительно есть, т.е. К следует брать гораздо больше 1.