Одной из характеристик целей является связанное с ней предпочтение на множестве исходов. При осознании цели возможно осознать, что лучше, что хуже по отношению к этой цели, т.е. возможно построить отношение предпочтений, которое включает в себя отношение доминирования (а>b а лучше b) и отношение безразличия (a~b, а сопоставимо с b) на множестве исходов А.
Существуют следующие методы выявления предпочтений:
1. Попарное сравнение объектов множества А. 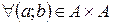 указывается наличие или отсутствие предпочтений:
указывается наличие или отсутствие предпочтений:
1 – доминирующий объект a>b;
0 – доминируемый объект a<b;
1/2 – безразличие (одинаковы) a~b;
«—» - несравнимость объектов (пустая клетка)
Кто-то выявил предпочтения на множестве (чай, кофе, компот, лимонад)
| чай | кофе | компот | лимонад | |
| чай | 1/2 | |||
| кофе | 1/2 | |||
| компот | 1/2 | 1/2 | ||
| лимонад | 1/2 | 1/2 |
2. Сравнение объектов по значениям показателей.
С точки зрения имеющейся цели необходимо выявить существенные показатели и сравнение объектов проводить на этом основании, например при установлении предпочтений среди кандидатов на должности существенные показатели это: уровень профессиональной подготовки, организационные способности, возраст и т.п. При выборе места работы учитываются следующие показатели: обстановка в коллективе, творчество в работе, заработная плата…
При сравнении показателей объектов необходимо учитывать технические показатели, стоимость, надежность. Первичная информация для сравнения задается таблицей.
| показатели объекты | P1 | P2 | … | Pm |
| a1 | P1(a1) | P2(a1) | … | Pm(a1) |
| a2 | P1(a2) | P2(a2) | … | Pm(a2) |
| … | … | … | … | … |
| an | P1(an) | P2(an) | … | Pm(an) |
Pj(ai) – значение j показателя для объекта ai; 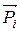 - вектор показателей для объекта а.
- вектор показателей для объекта а.
Для выявления предпочтений необходима система решающих правил позволяющая установить предпочитается объект ai объекту ak или нет. Единого, универсального решающего правила не существует, но для конкретных случаев на основе содержательных соображений производится выбор решающего правила:
1. Абсолютное предпочтение объекта множества А ai ≥ ak 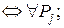 j=1;m (Pj(ai)≥Pj(ak)). Это отношение транзитивно, но является слабым, т.к различных сравнимых объектов в этом смысле мало.
j=1;m (Pj(ai)≥Pj(ak)). Это отношение транзитивно, но является слабым, т.к различных сравнимых объектов в этом смысле мало.
2. Предпочтение по правилу большинства.
3. Предпочитается по балльным оценкам объекта множества А. Для любого показателя устанавливается определенное число градаций. Низший балл=1 при переходе к следующему уровню оценка повышается на 1. Эта система применима для экспертных оценок. Число Lij – балл, которым j эксперт оценивает i объект. Выявление предпочтений является согласованием мнений экспертов.
4. Предпочтение по квазиупорядочиванию множества. Если для любого объекта множества А задана таблица показателей Pj, то любому показателю Pj присваивается вес λj выражающий значимость этого показателя. Тогда взвешенная сумма 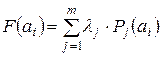 - суммарная оценка объекта ai.
- суммарная оценка объекта ai. 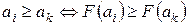 . Это самый сильный критерий из рассмотренных, т.к. приводится к линейному квазиупорядоченному множеству А, однако, труден при рассмотрении различных по своей природе показателей для которых установить вес непросто.
. Это самый сильный критерий из рассмотренных, т.к. приводится к линейному квазиупорядоченному множеству А, однако, труден при рассмотрении различных по своей природе показателей для которых установить вес непросто.
Итак, процедура выбора решающего правила не формализована и представляет собой сложную концептуальную проблему. Кроме того в процессе выбора оптимальных исходов возникает проблема выбора самого критерия оптимальности, т.е. известно что «лучше», но неизвестно, что значит «хорошо».
Выделяют 2 принципа оптимальности для задачи выбора объекта при заданном предпочтении:
1. Принцип недоминируемости. В качестве множества «хороших» объектов берется множество недоминируемых элементов множества А, т.е. таких элементов, для которых 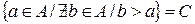 . Это множество называется С – ядром.
. Это множество называется С – ядром.
2. Принцип Неймана – Моргенштерна.
В качестве множества «хороших» объектов берется такое подмножество множества А, которое внутренне и внешне устойчиво. Множество 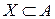 называется внешне устойчивым если для каждого элемента вне множества Х найдется такой элемент множества Х, который предпочтительней внешнего элемента, т.е.
называется внешне устойчивым если для каждого элемента вне множества Х найдется такой элемент множества Х, который предпочтительней внешнего элемента, т.е. 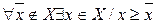
Ранжирование объектов – это расположение объектов в цепочку по убыванию их ценности, пригодности, важности от самого пригодного до самого плохого. Если есть равноценные объекты, в этом случае множество разбивается на классы равноценности, а классы в свою очередь ранжируются.
Простое ранжирование – это разбиение на 2 класса «плохие» и «хорошие» объекты. С точки зрения теории отношений, ранжирование есть задание линейкой транзитивной структуры доминирования безразличия или задание на множестве А линейного квазипорядка, при этом классы равносильных объектов являются классами эквивалентности. Геометрическое представление ранжирования – это диаграмма квазиупорядоченного множества, представляющая собой граф каждый класс эквивалентности это вершина, дуги указывают предпочтение.
Ранжирование согласованно предпочтениям проводится в 3 этапа:
1. Построение «грубого» ранжирования.
Разбиваем множество А на классы отношения взаимной достижимости в графе с помощью выделения контуров графа. В качестве линейного упорядочивания этих классов берем фактор – группы отношения ≥ по эквивалентности.
2. Построение тонкого ранжирования для каждого класса элементов, полученных при грубом ранжировании. Осуществляется по компонентам предельного вектора матрицы предпочтений. Пусть С – это класс эквивалентности отношения взаимной достижимости и отношения предпочтения, заданный с помощью матрицы доминирования и безразличия.
Всем элементам класса С присваивается номер от 1 до R. Рассмотрим матрицу 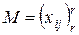 - часть матрицы доминирования и безразличий соответствующая элементам класса С.
- часть матрицы доминирования и безразличий соответствующая элементам класса С.
Силой n-го порядка i-го элемента называется число 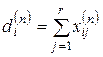 , а относительной силой n-го порядка i-го элемента называется число
, а относительной силой n-го порядка i-го элемента называется число 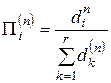
При неограниченном возрастании n 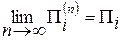 - относительная сила i-го элемента.
- относительная сила i-го элемента.
Вектор 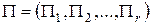 называется предельным вектором и является собственным вектором матрицы М соответствующим числу Перрона-Фробениуса. Наибольшее из неотрицательных собственных значений матрицы М есть число Перрона-Фробениуса.
называется предельным вектором и является собственным вектором матрицы М соответствующим числу Перрона-Фробениуса. Наибольшее из неотрицательных собственных значений матрицы М есть число Перрона-Фробениуса.
3. Совмещение грубого и тонкого ранжирования.
Нормированный собственный вектор, соответствующий числу Перрона-Фробениуса не меняется при элементарных преобразованиях матрицы: умножение на положительное число; сложение с матрицей kE, где 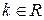 , E – единичная матрица.
, E – единичная матрица.
Пример: Ранжирование участников турнира на множестве М={a,b,c,d,e,f,g,h}
Задание линейного предпочтения матрицей N
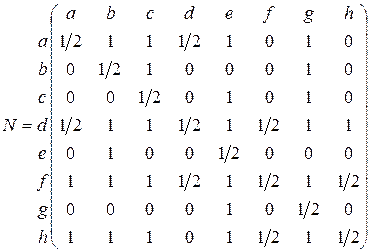



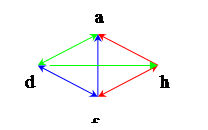
 Эту матрицу можно представить в виде графа G:
Эту матрицу можно представить в виде графа G:
в котором x>y ↔ →; x~y ↔ ↔

Первый шаг позволяет выделить 2 класса (грубое ранжирование).
I. C1={a; d; f; h} C2={c; g; e; b}; 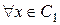
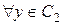 x≥y→C1≥C2
x≥y→C1≥C2
II. Тонкое ранжирование
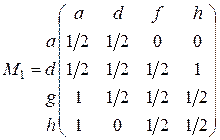
 |
G1: 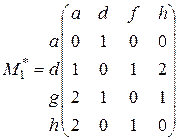
0 – несравнимость;
1 – эквивалентность;
2 – элемент i-ый лучше j-го;
Находим собственное значение для этой матрицы, решив уравнение.
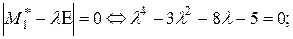
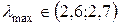
Находим собственные векторы, соответствующие этому λmax, решив систему уравнений:
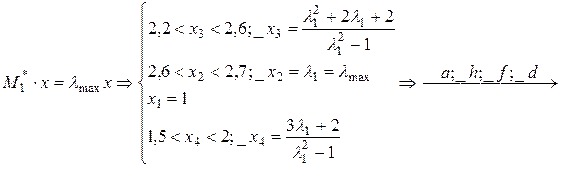
(Возрастание свойств по упорядочению координат собственного вектора);
Аналогично проводим упорядочение элементов в классе С2: 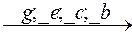
Ш. Т.о., искомое ранжирование элементов множества имеет вид:
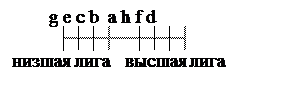

 2015-04-01
2015-04-01 1594
1594
