2015-04-01
863
1. Получить булевы формулы для функций: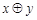 
, 
, 
.
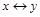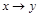2. С помощью эквивалентных преобразований привести к ДНФ формулу:
;
;
.
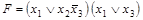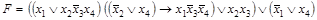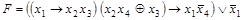3. Представить в виде совершенной ДНФ следующие функции:
; 
.
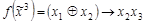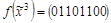4. С помощью преобразований вида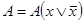 
, 
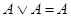перейти от заданной ДНФ 
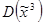к совершенной, если:
; 
; 
.
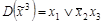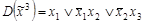5. С помощью соотношений вида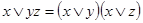 
преобразовать ДНФ из предыдущей задачи в КНФ.
6. Построить совершенную КНФ для каждой из функций задачи 3.
7. Доказать эквивалентность формул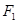 
и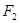 
.
, 
.
, 
.
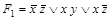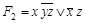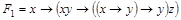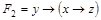8. Сколько существует линейных функций от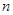 
переменных?
9. Построить полиномы для функции:
; 
;
; 
;
; 
.
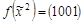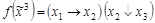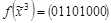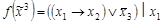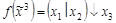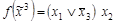10. Переменная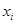 
является существенной переменной функции 
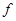тогда, и только тогда, когда 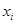явно входит в полином Жегалкина функции 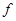. Получить полином Жегалкина функции 
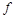и указать существенные переменные.
, 
, 
.
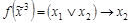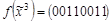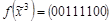11. Для нахождения полинома Жегалкина иногда используют метод неопределенных коэффициентов, состоящий в следующем. Рассматривается полином в виде (4.26) и для каждого набора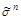 
составляется уравнение 
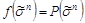. Решение этих уравнений дает коэффициенты 
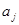полинома 
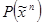. Например, задана логическая функция 
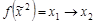, ее полином имеет вид
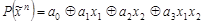
Составим систему уравнений.
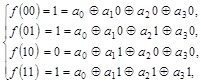
Находим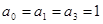 
, 
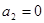. Таким образом,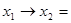 
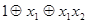. Напишите программу, находящую полином Жегалкина методом неопределенных коэффициентов, если исходная логическая функция задана вектором значений. Оцените трудоемкость программы, постройте график времени ее работы в зависимости от 
.
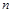12. Всякую логическую функцию 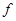можно записать в виде полинома, используя обычные арифметические операции умножения, сложения и вычитания. Для этого достаточно выразить 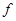через конъюнкцию и отрицание, а затем заменить подформулы вида 
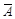на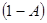 
и раскрыть скобки. Например, для функции 
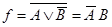эквивалентен полином 
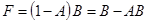. Выразить с помощью арифметических операций следующие функции:
; 
;
; 
.
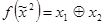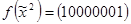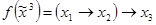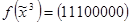Разработайте алгоритм построения бинарного графа логической функции заданной в ДНФ.
