Рассмотрим некоторый импликант функции 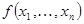 , являющийся конъюнкцией. Для удобства будем считать, что в него входят первые
, являющийся конъюнкцией. Для удобства будем считать, что в него входят первые 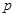 переменных, т.е., импликант имеет вид
переменных, т.е., импликант имеет вид 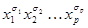 .
.
На всех наборах 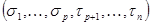 (при различных
(при различных 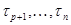 ) импликант
) импликант 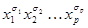 равен 1. Поэтому, функция
равен 1. Поэтому, функция 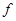 на этих наборах также обращается в 1, и в ее СДНФ присутствуют всевозможные конъюнкции вида
на этих наборах также обращается в 1, и в ее СДНФ присутствуют всевозможные конъюнкции вида 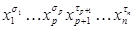 .
.
Осуществив склеивания по переменной 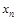 ,
,
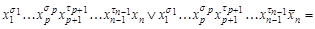
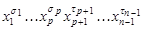 ,
,
из них можно получить всевозможные конъюнкции вида 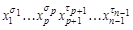 . Затем, произведя склеивания по переменной
. Затем, произведя склеивания по переменной 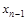 , придем к всевозможным конъюнкциям
, придем к всевозможным конъюнкциям 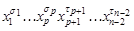 и т.д., пока не получим
и т.д., пока не получим 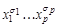 .
.
Таким образом, всякий импликант, имеющий вид конъюнкции, можно получить из конъюнкций СДНФ последовательным применением операции склеивания. Легко видеть, что верно и обратное: всякая конъюнкция, полученная таким образом, является импликантом 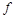 .
.
Отсюда можно сделать вывод, что все импликанты, имеющие вид конъюнкций, и только они, могут быть образованы в результате последовательного склеивания конъюнкций из СДНФ.
Пример 4.1. Пусть функция задана в СДНФ
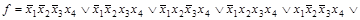
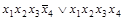 .
.
Получим все простые импликанты функции 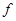 . Для этого необходимо произвести все возможные склеивания сначала конституент, а затем всех производных конъюнкций более низкого ранга и выполнить все возможные поглощения. Этот процесс иллюстрирует табл. 4.8. Таблица состоит из трех колонок, которые заполняются последовательно. В колонке 1 помещены конституенты единицы. Каждая конституента помечена номером (1-7). В колонке 2 содержатся конъюнкции ранга 3 (номера 8-13), полученные в результате проведения всех возможных склеиваний конституент. Если
. Для этого необходимо произвести все возможные склеивания сначала конституент, а затем всех производных конъюнкций более низкого ранга и выполнить все возможные поглощения. Этот процесс иллюстрирует табл. 4.8. Таблица состоит из трех колонок, которые заполняются последовательно. В колонке 1 помещены конституенты единицы. Каждая конституента помечена номером (1-7). В колонке 2 содержатся конъюнкции ранга 3 (номера 8-13), полученные в результате проведения всех возможных склеиваний конституент. Если  и
и 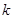 конституенты склеились, используется запись
конституенты склеились, используется запись 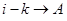 , где
, где 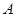 – результат склеивания. Конституенты, поглощаемые конъюнкциями колонки 2, помечаются значком
– результат склеивания. Конституенты, поглощаемые конъюнкциями колонки 2, помечаются значком  . В колонке 3 находятся конъюнкции ранга 2, полученные путем проведения всех возможных склеиваний конъюнкций из колонки 2. Поглощаемые ими конъюнкции из колонки 2 отмечаются значком
. В колонке 3 находятся конъюнкции ранга 2, полученные путем проведения всех возможных склеиваний конъюнкций из колонки 2. Поглощаемые ими конъюнкции из колонки 2 отмечаются значком  . Конъюнкции из колонки 3 не склеиваютя. Конституенты и конъюнкции более низкого ранга, не участвовавшие в склеивании (не отмеченные значком
. Конъюнкции из колонки 3 не склеиваютя. Конституенты и конъюнкции более низкого ранга, не участвовавшие в склеивании (не отмеченные значком  ), являются простыми импликантами, образующими сокращенную ДНФ функции
), являются простыми импликантами, образующими сокращенную ДНФ функции 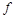
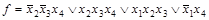
Таблица 4.8
| 1) | 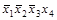
| 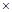
| 8) | 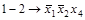
| 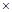
| 15) | 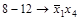
|
| 2) | 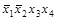
| 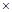
| 9) | 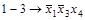
| 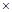
| 16) | 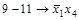
|
| 3) | 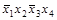
| 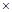
| 10) | 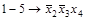
| |||
| 4) | 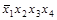
| 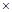
| 11) | 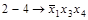
| 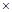
| ||
| 5) | 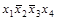
| 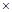
| 12) | 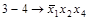
| 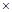
| ||
| 6) | 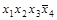
| 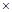
| 13) | 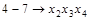
| |||
| 7) | 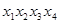
| 
| 14) | 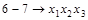
|
 2015-04-01
2015-04-01 400
400








