Совершенная полиномиальная нормальная форма. Полином Жегалкина. Линейные функции

Пусть функция 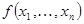представлена в СДНФ 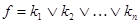, где 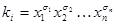, 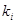различны. По соотношению (4.22) 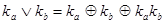. Однако конъюнкция двух различных конституент единицы 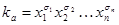и 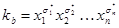равна 0, так как 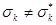, по крайней мере для одного 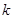, 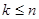и тогда 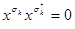и, следовательно, 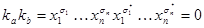. Т.о.,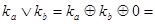 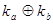. Из данной формулы следует, что в СДНФ можно заменить операцию дизъюнкции операцией сумма по модулю 2. Такая форма называется совершенной полиномиальной нормальной формой (СПНФ).

Пример. Получить СПНФ функции .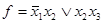

Для получения СПНФ представим функцию в СДНФ:

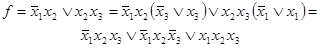
Тогда в СПНФ функция запишется в следующем виде:

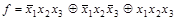
Если в произвольной формуле алгебры Жегалкина раскрыть скобки по правилу (4.18) и произвести все возможные упрощения по соотношениям (4.19) и (4.20), то получится формула, имеющая вид суммы произведений, то есть, полинома по модулю 2. Такая формула называется полиномом Жегалкина. Полином Жегалкина имеет вид

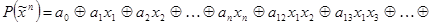
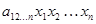, (4.26)

где .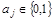

Пример. Получить полином Жегалкина функции .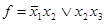

1. В СПНФ функция представляется следующим образом 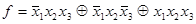(см. предыдущий пример). Избавимся от отрицаний, используя соотношение (4.21):

.

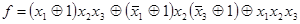Раскрыв скобки и применив формулы (4.19) и (4.20), получим

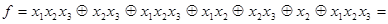
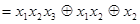
2. Используя формулы (4.22) и (4.21), получаем

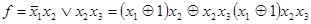
Раскрыв скобки, и применив формулы (4.19) и (4.20), получим

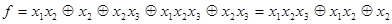
Для получения полинома из произвольной формулы сначала, обычно, строят эквивалентную формулу над множеством связок 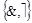, а затем, получают из нее полином.

Пример. Получить полином Жегалкина функции .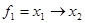

Используя определение элементарных функций (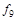 в табл. 4.6), получим СКНФ импликации: 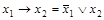. Далее получим полином: .

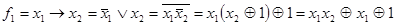Если полином Жегалкина функции имеет вид

,

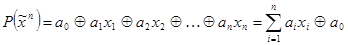то функция называется линейной.

Пример 4.5. Определить, является ли функция 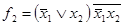линейной:

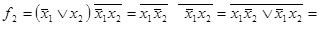
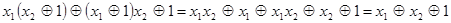
Таким образом, в полиноме функции 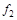отсутствуют конъюнкции переменных, следовательно, функция линейна. В предыдущем примере, в полиноме функции 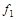присутствовала конъюнкция переменных 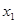и 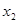, т.е. 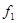– нелинейная функция.

Теорема 4.3. Для всякой логической функции существует полином Жегалкина, и притом единственный.

Доказательство: Существование полинома уже доказано. Для доказательства единственности, покажем, что между множествами всех функций от 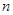переменных и множеством всех полиномов Жегалкина от 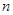переменных существует взаимно однозначное соответствие. Число различных членов (то есть конъюнкций переменных) полиномов от 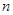переменных равно числу всех подмножеств из 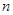элементов, то есть 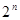(пустому подмножеству соответствует член 1). Число различных полиномов, которые можно образовать из этих конъюнкций, равно числу всех подмножеств множества конъюнкций, то есть 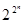(пустому подмножеству конъюнкций соответствует полином 0). Таким образом, число всех полиномов Жегалкина от 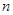переменных равно числу всех функций от 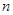переменных. Так как разным функциям соответствуют разные полиномы (одна и та же формула не может представлять две разные функции), то, тем самым, между множествами функций и полиномов от 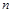переменных установлено взаимное однозначное соответствие, что и доказывает единственность полинома для каждой функции. Теорема доказана.

На основании теоремы 4.3 можно проверять эквивалентность формул. Для этого, каждую формулу преобразуют в полином Жегалкина и производят сравнение полученных полиномов.