Минимизация булевых функций

Отметим, что реально формуле соответствует соединение элементов, реализующих исходные функции (логическая схема). Каждой формуле соответствует своя логическая схема (см. гл. 8).

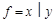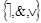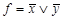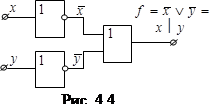
Например, функция штрих Шеффера может быть представлена двумя формулами над множеством связок : и 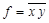. Первой формуле соответствует схема, представленная на рис.4.4, второй – на рис.4.5¹⁾. Схема, соответствующая второй формуле, содержит на один элемент меньше, чем схема, соответствующая первой формуле, следовательно, она более предпочтительна. Задача поиска формулы, соответствующей наиболее простой схеме (задача минимизации логической функции), представляет большой практический интерес.

Общая задача минимизации может быть сформирована следующим образом: найти аналитическое выражение заданной логической функции в форме, содержащей минимально возможное число связок. Следует отметить, что в общей постановке данная задача пока не решена, однако, достаточно хорошо исследована для булевых функций в классе дизъюнктивно-конъюнктивных нормальных форм.

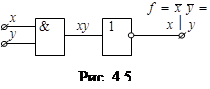Дадим основные определения.

Элементарной конъюнкцией называется конъюнкция конечного числа различных между собой логических переменных, каждая из которых может иметь или не иметь отрицания.

Рангом элементарной конъюнкции называется число переменных в данной конъюнкции.

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций.

Минимальной дизъюнктивной нормальной формой (МДНФ) логической функции называется ДНФ, содержащая наименьшее число букв (по отношению ко всем другим ДНФ, представляющим заданную логическую функцию).

Логическая функция 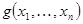называется импликантом функции 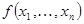, если для всякого набора 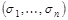значений аргументов выполнено неравенство 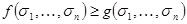. Это условие может быть эквивалентно переписано в виде

.

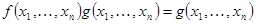Импликант называется простым, если он представляет собой конъюнкцию переменных (возможно, с отрицаниями) и любая конъюнкция, получаемая из него в результате вычеркивания каких-либо переменных, импликантом не является.

В качестве примера рассмотрим функцию .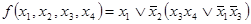

Функция 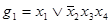является импликантом, ибо

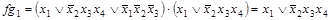
(мы воспользовались соотношением .

Поскольку 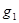не есть конъюнкция, импликант 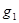не простой. Конъюнкция 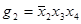также является импликантом. Если из нее вычеркнуть переменную 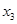, полученная конъюнкция 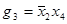снова будет импликантом, ибо

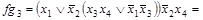
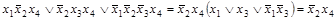
Отсюда следует, что импликант 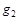не является простым. Легко проверить, что конъюнкци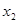и и 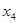, полученные из 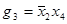вычеркиванием одной переменной, импликантами не будут. Поэтому 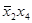представляет собой простой импликант.

Утверждение. Любая логическая функция 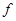эквивалентна дизъюнкции всех своих простых импликантов.

Дизъюнкция всех простых импликантов логической функции называется ее сокращенной ДНФ.

Приведенное утверждение ясно, если рассмотреть геометрическую интерпретацию логической функции в виде гиперкуба. В этом случае можно дать следующее определение импликанта. Функция 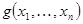является импликантом для 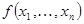, если соответствующее ей множество вершин куба содержится во множестве вершин для . Всякая конъюнкция 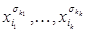задает подкуб, представляющий собой множество вершин 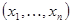, для которых 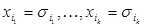, а значения остальных 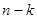компоненты могут быть выбраны произвольно. Подкуб, соответствующий конъюнкции длины 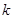, содержит 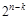вершин. 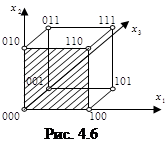В частности, подкуб для конъюнкции длины 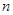вырождается в вершину. На рис. 4.6 заштрихован подкуб, соответствующий конъюнкции 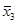(он представляет собой грань 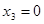). Простой импликант определяет подкуб, все вершины которого принадлежат множеству единичных вершин функции, и такой, что он не содержится ни в каком большем подкубе, обладающем этим свойством. Такие подкубы называют максимальными. Всякая ДНФ задает покрытие множества единичных вершин функции подкубами, соответствующими ее конъюнкциям. Всякая сокращенная ДНФ задает покрытие множества единичных вершин функции максимальными подкубами. На этом языке данное утверждение становится очевидным.

Сокращенная ДНФ логической функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.

Устранение лишних простых импликантов из сокращенной ДНФ логической функции не является однозначным процессом, т.е., логическая функция может иметь несколько тупиковых форм. Тупиковые ДНФ, содержащие минимальное число букв, являются минимальными. Минимальных ДНФ логической функции тоже может быть несколько.

Все методы минимизации практически отличаются лишь на первом этапе – этапе получения сокращенной ДНФ. Второй этап - получение минимальной (или одной из тупиковых) ДНФ идентичен для всех методов.

В данной главе будут рассмотрены два метода минимизации полностью определенных функций и метод минимизации частичных функций. Все методы функционируют в классе ДНФ. Путем применения принципа двойственности эти методы могут быть обобщены для КНФ.