2015-04-01
883
1.1.1 Методы эквивалентных преобразований.
Замена нескольких последовательно соединенных сопротивлений одним эквивалентным: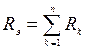 
.
Напряжение при последовательном соединении распределяется прямо пропорционально этим сопротивлениям:
, 
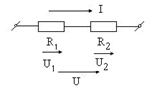
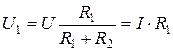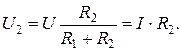
Замена нескольких параллельно соединенных сопротивлений одним эквивалентным: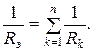 
Для двух сопротивлений: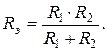 
Токи в ветвях с параллельным соединением двух сопротивлений:
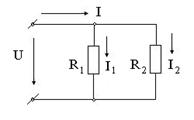
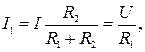
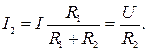
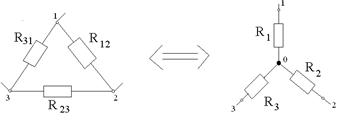
Формулы преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений и наоборот:
; 
; 
;
; 
; 
.
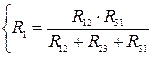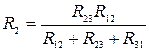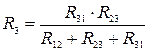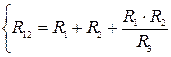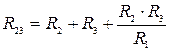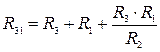1.1.2 Методы расчёта разветвленных электрических цепей постоянного тока.
Законы Кирхгофа
Первый закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю: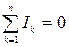 
.
Второй закон Кирхгофа: алгебраическая сумма напряжений на элементах любого замкнутого контура электрической цепи, исключая ЭДС, равна алгебраической сумме ЭДС этого же контура: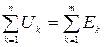 
. Напряжения на линейных резисторах заменяют произведением 
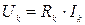на основании закона Ома для участка цепи.
Для записи уравнений по второму закону Кирхгофа в систему уравнений выбирают независимые контуры, не содержащие источников тока.
Уравнения по методу контурных токов записываются в виде:
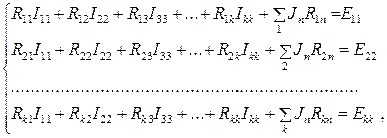
где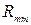 
– собственное сопротивление контура m, равное сумме сопротивлений ветвей, входящих в контур m;
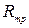– общее сопротивление контуров m и р, равное сумме сопротивлений смежных ветвей контуров m и р;
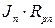– напряжение на сопротивлении 
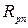общей ветви контура р и контура n, содержащего источник тока 
;
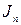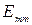– алгебраическая сумма ЭДС контура р.
Потенциал одного из узлов принимают равным нулю. Для определения потенциалов остальных узлов составляют систему уравнений:
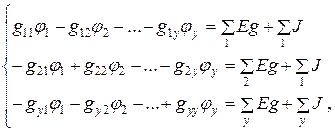
где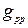 
– собственная узловая проводимость узла р, равная сумме проводимостей ветвей, присоединенных к узлу р;
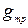– общая узловая проводимость узлов р и m, равная сумме проводимостей ветвей, соединяющих узлы р и m;
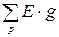– алгебраическая сумма произведений ЭДС ветвей, присоединённых к узлу р на проводимости этих ветвей;
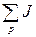– алгебраическая сумма токов источников тока, присоединённых к узлу р.
Если электрическая схема содержит ветвь с идеальным источником ЭДС Е и с сопротивлением, равным нулю, то при составлении уравнений по методу узловых потенциалов к нулю приравнивают потенциал одного из узлов, к которому присоединена данная ветвь. Тогда потенциал другого узла этой ветви будет равен + E или – E, в зависимости от направления ЭДС.
