Матрица 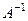 называется обратной для квадратной матрицы
называется обратной для квадратной матрицы  , если
, если 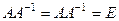 . Квадратная матрица
. Квадратная матрица  имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Квадратная матрица
имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Квадратная матрица  , определитель которой не равен нулю, имеет единственную обратную матрицу
, определитель которой не равен нулю, имеет единственную обратную матрицу
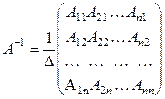 ;
;
где 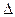 – определитель матрицы
– определитель матрицы  ;
;
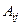 – алгебраическое дополнение элемента
– алгебраическое дополнение элемента 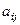 матрицы
матрицы  .
.
2. n -мерные векторы
2.1. Линейные операции над n -мерными векторами
В геометрии вектором в пространстве называется направленный отрезок. В фиксированной системе координат каждый вектор а однозначно определяется своими координатами:
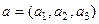 , (1)
, (1)
где 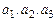 называются координатами вектора a.
называются координатами вектора a.
Если 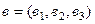 – какой-либо другой вектор, то
– какой-либо другой вектор, то
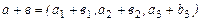 (2)
(2)
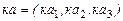 , (3)
, (3)
где 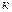 – число.
– число.
Сложение векторов и умножение вектора на число называются линейными операциями над векторами.
Обобщим понятие вектора следующим образом: назовем последовательность n чисел 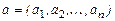 n -мерным вектором. Число
n -мерным вектором. Число 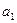 называется первой координатой вектора
называется первой координатой вектора 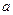 ;
; 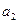 – второй координатой и т.д., а число n (количество координат) называется размерностью вектора а.
– второй координатой и т.д., а число n (количество координат) называется размерностью вектора а.
Если 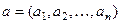 ,
, 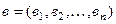 , то
, то
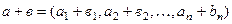 ,
, 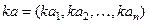 .
.
Два n -мерных вектора:
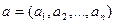 ,
, 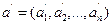 ,
,
считаются равными только тогда, когда равны их соответствующие координаты 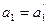 ,
, 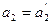 ,…,
,…, 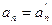 .
.
Очевидно, что для любого вектора а:
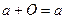 , где
, где 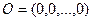 .
.
Вектор 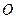 называется нулевым.
называется нулевым.
Вектор (-1) 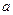 называется противоположным вектору
называется противоположным вектору 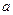 и обозначается
и обозначается 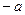 , т.е.
, т.е. 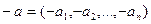 . Ясно, что
. Ясно, что 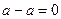 и
и 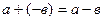 .
.
Так как операции над n-мерными векторами определяются через операции над их координатами, то свойства арифметических операций справедливы и для операций над векторами.
1. 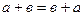 (сложение коммутативно).
(сложение коммутативно).
2. 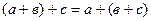 (сложение ассоциативно).
(сложение ассоциативно).
3. 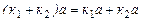
 ;
; 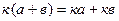 (сложение дистрибутивно, где
(сложение дистрибутивно, где 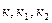 – некоторые вещественные числа).
– некоторые вещественные числа).
2.2. Скалярное произведение и длина n -мерных векторов
Как известно из геометрии, если векторы а и 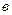 заданы своими координатами
заданы своими координатами 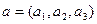 и
и 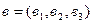 , то их скалярное произведение
, то их скалярное произведение 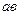 определяется по формуле:
определяется по формуле:
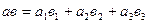 .
.
По аналогии скалярным произведением n -мерных векторов 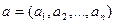 ,
, 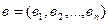 называется число
называется число 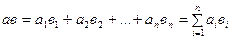 .
.
Некоторые свойства произведения чисел справедливы и для скалярного произведения векторов:
1. 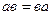 .
.
2. 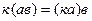 , где
, где 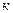 число.
число.
3. 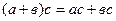 .
.
4. 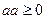
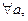 причем
причем 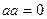 тогда и только тогда, когда
тогда и только тогда, когда 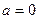 (нулевой вектор).
(нулевой вектор).
Длиной n -мерного вектора 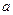 называется число
называется число 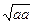 . Длина вектора
. Длина вектора 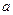 обозначается
обозначается 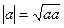 .
.
Из 4-го свойства скалярного произведения векторов вытекает, что каждый 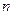 -мерный вектор
-мерный вектор 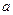 обладает длиной, причем нулевой вектор
обладает длиной, причем нулевой вектор 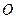 , является единственным вектором, длина которого равна нулю.
, является единственным вектором, длина которого равна нулю.
Если а и в 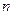 -мерные векторы, то справедливы следующие числовые соотношения:
-мерные векторы, то справедливы следующие числовые соотношения:
1) 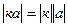 ,
, 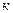 -число
-число
2) 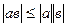 (неравенство Коши-Буняковского)
(неравенство Коши-Буняковского)
3) 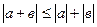 (неравенство треугольника)
(неравенство треугольника)
Вектор называется нормированным, если его длина равна 1. Каждый вектор 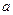 можно нормировать, т.е. умножить на число
можно нормировать, т.е. умножить на число 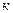 , чтобы вектор
, чтобы вектор 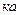 был нормированным.
был нормированным.
В самом деле:
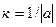 ,
,
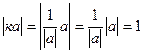 .
.
2.3. Угол между n- мерными векторами
Из неравенства Коши-Буняковского
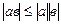
следует
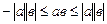 ,
,
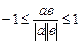 .
.
Углом между 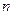 -мерными векторами
-мерными векторами 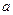 и
и 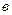 называется значение; которое получается из решения уравнения:
называется значение; которое получается из решения уравнения:
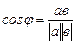 (4)
(4)
и принадлежит отрезку 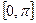 .
.
Причем решение единственно при любых 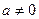 и
и 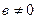 . Следовательно, и угол между векторами
. Следовательно, и угол между векторами 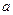 и
и 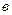 определен однозначно.
определен однозначно.
Перепишем соотношение (4) в виде
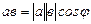 ,
,
отсюда следует, что скалярное произведение векторов 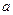 и
и 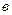 равно произведению длин этих векторов на косинус угла между ними.
равно произведению длин этих векторов на косинус угла между ними.
Геометрическая характеристика векторов – длина вектора и угол между векторами – позволяет сформулировать критерий равенства n -мерных векторов.
Теорема. Ненулевые n -мерные вектора а и 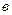 равны тогда и только тогда,когда угол между ними равен нулю и длины этих векторов равны.
равны тогда и только тогда,когда угол между ними равен нулю и длины этих векторов равны.
 2015-04-01
2015-04-01 584
584








