Пусть дана система n - мерных векторов 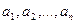 выбираем n – произвольных чисел
выбираем n – произвольных чисел 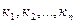 .
.
Вектор 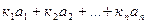 называется линейной комбинацией векторов
называется линейной комбинацией векторов 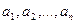 с коэффициентами
с коэффициентами 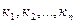 .
.
Пусть теперь наряду с векторами 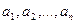 дан еще n -мерный вектор
дан еще n -мерный вектор 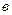 . Будем говорить, что вектор
. Будем говорить, что вектор 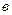 линейно выражается через векторы
линейно выражается через векторы 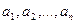 , если он равен некоторой линейной комбинации векторов
, если он равен некоторой линейной комбинации векторов 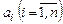 , т.е. найдется такой набор чисел
, т.е. найдется такой набор чисел 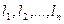 , что
, что
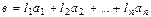 . (5)
. (5)
В этом случае будем говорить также, что вектор 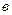 разлагается по векторам
разлагается по векторам 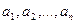 . Числа
. Числа 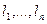 называются коэффициентами разложения вектора
называются коэффициентами разложения вектора 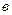 по системе
по системе 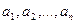 .
.
Разложение 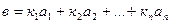 считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один
считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один 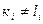 ).
).
Справедливы следующие утверждения:
1. Нулевой вектор 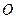 разлагается по каждой системе векторов
разлагается по каждой системе векторов 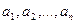
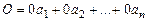 .
.
2. Если вектор 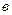 разлагается по части системы векторов
разлагается по части системы векторов 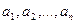 , то он разлагается и по всей системе векторов.
, то он разлагается и по всей системе векторов.
Предположим, что
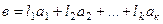 , где
, где 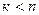 ,
,
тогда 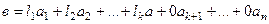 .
.
3. Каждый 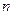 -мерный вектор
-мерный вектор 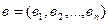 разлагается по диагональной системе
разлагается по диагональной системе 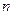 - мерных векторов:
- мерных векторов:
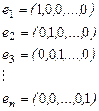
с коэффициентами, которые равны координатам вектора 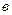 .
.
В самом деле
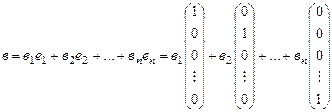 .
.
4. Если вектор 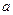 разлагается по системе векторов
разлагается по системе векторов 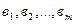 , а каждый вектор этой системы разлагается по системе векторов
, а каждый вектор этой системы разлагается по системе векторов 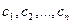 , то вектор
, то вектор 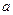 разлагается по системе векторов
разлагается по системе векторов 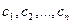 .
.
Из условия следует, что
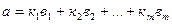
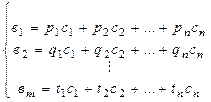
После подстановки получаем:
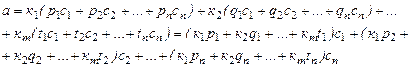
Т.е. вектор 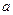 разлагается по векторам
разлагается по векторам 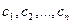 .
.
 2015-04-01
2015-04-01 1015
1015
