Используя введенные операции над векторами, запишем систему линейных уравнений:
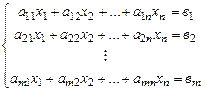 (1)
(1)
в векторной форме. Обозначим 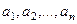 столбцы коэффициентов при неизвестных
столбцы коэффициентов при неизвестных
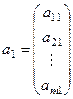 ,
, 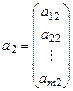 ,…,
,…, 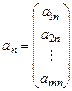 ;
;  .
.
Тогда систему (1) можно представить в виде:
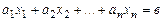 (2)
(2)
Уравнение (2) называется векторной формой системы линейных уравнений (1).
Последовательность чисел 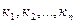 называют решением системы (2), если
называют решением системы (2), если 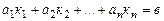 – верное векторное равенство.
– верное векторное равенство.
Пусть n -мерный вектор (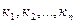 ) является решением системы (1). Тогда ясно, что для разложения вектора
) является решением системы (1). Тогда ясно, что для разложения вектора 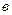 по системе
по системе 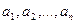 достаточно найти решение системы линейных уравнений (2).
достаточно найти решение системы линейных уравнений (2).
Пример. Дана система векторов 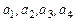 и вектор
и вектор 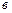
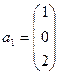 ;
; 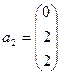 ;
; 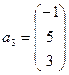 ;
; 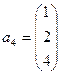 ;
; 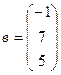 .
.
Пример. Выяснить разлагается ли вектор 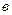 по системе векторов
по системе векторов 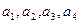 .
.
Для этого необходимо решить систему уравнений
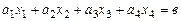 .
.
Имеем:
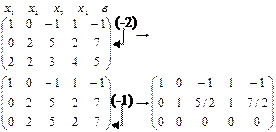 |
Получили систему уравнений:
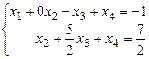 ,
,
которая эквивалентна исходной (т.е. имеет то же множество решений). Выразим главные неизвестные 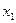 и
и 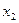 через свободные
через свободные 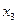 .
. 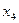 . Получим общее решение:
. Получим общее решение:
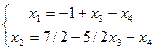 .
.
Достаточно положить свободным неизвестным 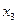 и
и 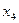 произвольные значения и получить разложение вектора
произвольные значения и получить разложение вектора 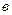 по системе векторов
по системе векторов 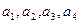 .
.
Пример. 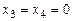 , тогда
, тогда 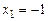 ,
, 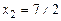 .
.
Следовательно:
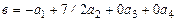 .
.
Если же 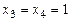 , тогда
, тогда 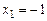 ,
, 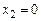
и 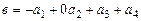 .
.
 2015-04-01
2015-04-01 12924
12924
