2015-04-01
807
Система векторов а1, а2, …, аn называется линейно зависимой, если система уравнений
a1x1 + a2x2 + … + аnxn = 0 (1)
имеет ненулевое решение, если же система уравнений не имеет ненулевых решений, то система векторов a1, a2 …, an называется линейно независимой.
Будем говорить, что набор чисел k1, k2, … kn является ненулевым, если хотя бы одно из чисел K отлично от нуля.
Для линейно зависимых систем векторов (линейно независимых) справедливы следующие утверждения:
1. Система векторов, состоящая из одного вектора a ≠ 0 линейно независима.
В самом деле, из любого соотношения кa = 0 и a ≠ 0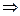 
к = 0, что и означает линейную независимость системы.
2. Диагональная система векторов
; 
; …, 
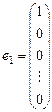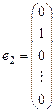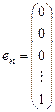
линейно независима. Запишем систему уравнений
e 1 x 1 +e 2 x 2 + … e n x n = 0(2)
в виде таблицы
| x 1 | x 2 | … | xn | |
| … | ||||
| … | ||||
| … | … | … | … | |
| … |
Откуда ясно, что система уравнений (2) имеет единственное решение x 1=0; x 2=0… xn =0, т. е. не имеет не нулевых решений и поэтому диагональная система векторов линейно независима.
|
|
|
1. Система векторов a 1, a 2 …, an линейно зависима, если хотя бы один из векторов системы разлагается по остальным векторам этой системы.
Пусть какой-нибудь вектор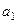 
разлагается по остальным векторам системы
a1=l2a2+l3a3+…+lnan (3)
Представим (3) в виде
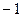a1+l2a2+l3a3…+lnan=0.
Так как набор чисел (решение) 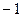, l2, l3…, ln – ненулевой, система векторов a1, a2,…,an –линейно зависима.
2. Система m мерных векторов a1, a2,…, an линейно зависима, если n > m.
Действительно, система уравнений
a1x1+a2x2+…+anxn=0 (4)
содержит m уравнений и n неизвестных.
Так как по условию n > m, то из утверждения «система линейных однородных уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение» вытекает, что система уравнений (4) обладает ненулевым решением. Следовательно, система векторов a1, a2, …, an линейно зависима.
