1. Непосредственно из определений видно, что каждая система векторов либо линейно зависима, либо линейно независима.
2. Если часть системы векторов a1, a2, …, an линейно зависима, то и вся система линейно зависима.
Допустим, что часть, состоящая из векторов a1, a2,…, ap линейно зависима, т. е. k1a1+k2a2+…kpap= 0и k1, k2…kp ненулевой набор чисел. Тогда соотношение
k1a1+k2a2+…+ kpap+ 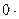 ap+1+
ap+1+ 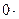 ap+2+…+
ap+2+…+ 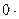 an= 0
an= 0
выполняется с ненулевым набором чисел. k1, k2…kp, 0,…,0 – что и означает линейную зависимость системы a1,…,an.
3. Если система векторов a1, …, an линейно независима, то и любая ее часть линейно независима.
Докажем это свойство от противного. Предположим, что часть системы линейно зависима. Тогда из свойства (2) следует, что и вся система линейно зависима, однако это противоречит условию. Следовательно, любая часть данной системы линейно не зависима.
4. Если система векторов a1, a2,…, an линейно зависима, то хотя бы один из векторов этой системы разлагается по остальным ее векторам.
5. Если система векторов a1, a2,…, a n линейно зависима, а ее часть a1 …, an-1 линейно независима, то вектор an разлагается по векторам a 1, a 2, …, an-1.
Пример. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой.
a 1=(3, 5, 1, 4 ), a 2=(-2, 1,-5, -7 ), a 3= (-1, -2, 0, -1 )
Преобразуем систему линейных уравнений
a1x1+a2x2+a3x3=0 методом Гаусса, (столбец свободных членов состоит только из нулей и не изменяется в процессе преобразований, поэтому его можно не записывать)
| X1 | X2 | X3 | ||||
| -2 | -1 | |||||
  -2 -2 | ||||||
| -5 | ||||||
| -7 |   -1 -1 | |||||
  -3 -3 |
| |||||
| -1 | ||||||
  1 1 | -5 | |||||
 1 1 | -5 |
| X1 | X2 | X3 |
| -13 | ||
| -5 | ||
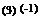
Общее решение уравнения имеет вид
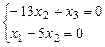
Получаем эквивалентную систему:
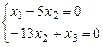
Эта система имеет ненулевое решение (5, 1, 13). Следовательно, векторы a 1, a 2, a3 линейно зависимы.
Пример. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой.
a1 =(-20, -15, -4 ); a2 =(-7, -2, -4 ); a3 = (3, -1, -2).
Преобразуем систему линейных уравнений
x 1 a 1+ x 2 a 2+ x 3 a 3=0
методом Гаусса
| X3 | X2 | X3 | ||||
| -20 | -7 |   3 3 | ||||
| -15 | -2 |   -1 -1 | ||||
| -4 | -4 | -2 | ||||
| -26 | -13 | |||||
| -13 | ||||||
  2 2 |
| |||||
 2 2 |   0 0 | |||||
| -13 | ||||||
| -2 |   1 1 | |||||
| ||||||
|
Общее решение системы имеет вид x 1 = 0; x 2 = 0;. x 3 = 0.
Эта система не имеет ненулевых решений, таким образом, система векторов a 1, а 2, а 3 линейно независима.
 2015-04-01
2015-04-01 862
862








