Расчетная схема задачи представлена на рисунке 5. Размеры конструкции (мм): l 1=300 мм, l 2=500 мм, d1=240 мм, d2=30 мм, D1=200 мм, t1=40 мм.
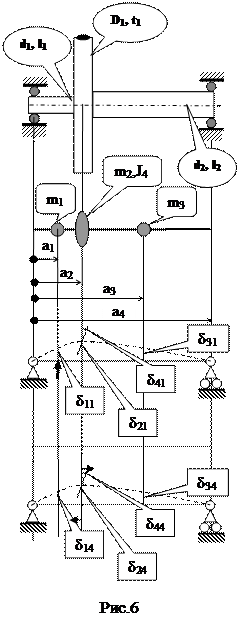 Размеры расчетной схемы стержня: а1=150 мм, а2=320 мм, а3=590 мм, а4=840 мм.
Размеры расчетной схемы стержня: а1=150 мм, а2=320 мм, а3=590 мм, а4=840 мм.
Расчетные моменты инерции сечений:
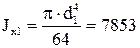 мм4
мм4
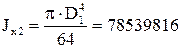 мм4
мм4
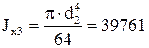 мм4
мм4
Расчетные меры инерции в 4-х массовой системе:
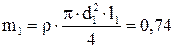
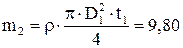
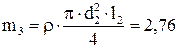
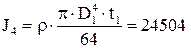 мм4
мм4
Параметры материала:
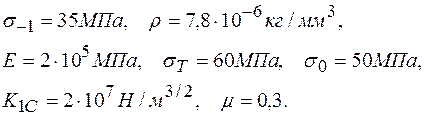 Расчет критической скорости вращения вала
Расчет критической скорости вращения вала
Воспользуемся алгоритмом определения собственных частот колебаний стержня [1].
· Распределим массы и жесткости по длине в соответствии с чертежом и вычислим взаимные податливости в полученной четырехмассовой систем. Воспользуемся для этого шаблоном [1] численного интегрирования дифференциальных уравнений прямого стержня. В рассматриваемом примере получаем следующие значения в м/Н, 1/Н·м.
| δ11 | δ21 | δ31 | δ41 | δ21 | δ22 | δ23 | δ24 |
| 1.87E-06 | 2.26E-06 | 1.28E-06 | 2.53E-09 | 2.26E-06 | 2.98E-06 | 1.84E-06 | 1.96E-09 |
| δ31 | δ32 | δ33 | δ34 | δ41 | δ42 | δ 43 | δ44 |
| 1.28E-06 | 1.84E-06 | 1.42E-06 | -3.11E-10 | 2.53E-09 | 1.96E-09 | -3.11E-10 | 1.55E-11 |
· Воспользуемся шаблоном, в котором формируется характеристический определитель [1]. В примере удается найти два положительных его корня 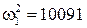 1/сек2,
1/сек2, 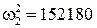 1/сек2. Откуда вычисляем две низшие критические круговые частоты
1/сек2. Откуда вычисляем две низшие критические круговые частоты
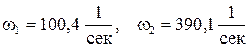 ;
;
критические обороты 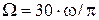 , т.е.
, т.е.
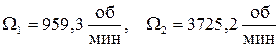 .
.
Расчет критической скорости вращения по методу допускаемых напряжений в диске
Для диска, выполненного заодно целое с валом, имеем максимальные напряжения  при
при 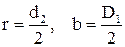 , т.е.
, т.е. 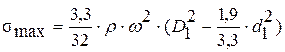 .
.
Принимаем цикл нагружения пульсирующим, т.е. 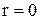 . Тогда
. Тогда
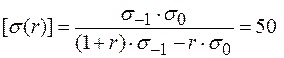 МПа.
МПа.
Из условия 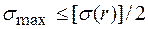 получаем
получаем 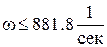 ,
, 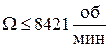 .
.
Расчет допустимого размера трещины
Принимаем предельную скорость вращения 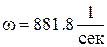 . Тогда в указанной точке на поверхности диска
. Тогда в указанной точке на поверхности диска 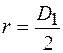 нормальные напряжения
нормальные напряжения
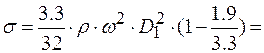 10,6 МПа,
10,6 МПа, 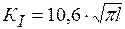 ,
,
и из равенства 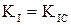 вычисляем критическую длину трещины
вычисляем критическую длину трещины
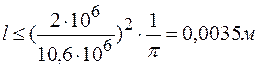 .
.
 2015-04-01
2015-04-01 340
340








