Основные категории статистики 2 страница

Кумулята отражает характер нарастания частот от группы к группе и строится по накопленным частотам (или частостям). Для построения кумуляты на ось абсцисс наносят значения вариантов — точки для дискретного ряда или интервалы для интервального — и из каждой точки или верхней границы интервала восстанавливают перпендикуляр (ординату), высота которого соответствует накопленной частоте (или частости) данного варианта; затем вершины перпендикуляров последовательно соединяются плавной линией.

2.3 Абсолютные и относительные величины

Абсолютные статистические величины выражают либо уровни, характеризующие состояние на определенный момент (среднесписочную численность, стоимость имущества на определенную дату), либо результаты процессов за определенный период (продукция предприятий, затраты труда и материалов). По своему содержанию абсолютные статистические величины могут быть сравнительно простыми (численность предприятий, рабочих) или сложными, характеризующими экономические категории (понятия), такие как прибыль, себестоимость, производительность труда. Абсолютные величины всегда числа именованные. В зависимости от показателей изучаемого явления и задач исследования эти величины выражаются в различных единицах измерения: натуральных (численность, меры длины, веса, объема), денежных или стоимостных и трудовых (человеко-час, человеко-день, человеко-год и т.п. для измерения затрат труда на выполнение какой-либо работы).

Относительные величины получают в результате сравнения двух показателей. Знаменатель отношения, т.е. та величина, с которой сравнивают другую, называется основанием или базой сравнения. Если основание единица, то относительная величина — коэффициент, если основание 100, то относительная величина — процент, если основание — 1000, то относительная величина измеряется в промилле.

Различают следующие виды относительных величин: относительные величины планового задания, выполнения плана, структуры, координации, интенсивности, уровня экономического развития, динамики и сравнения.

Относительные величины планового задания представляют собой отношение величины показателя, который определен на планируемый период, к величине, принятой за базу сравнения.

Относительные величины выполнения плана дают количественную характеристику выполнения плановых заданий и выражаются в процентах. Исчисляют эту относительную величину по формуле:

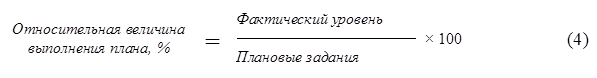
Относительные величины структуры представляют собой соотношение размеров частей и целого и выражаются в долях единицы (коэффициентах) и процентах. Пример расчета относительных величин структуры показан в табл.2.

Таблица 2

Структура промышленно-производственного персонала фирмы

Категории персонала	Базисный период	Отчетный период
Чел.	%	Чел.	%
Руководители и специалисты Служащие Рабочие		17.4 25.3 57.3		16.4 23.6 60.0
Итого

Как показывает табл.2, в отчетном периоде в фирме увеличилась доля рабочих и в два раза снизилась доля руководителей и специалистов. Такого рода изменения называют структурными сдвигами.

Относительные величины координации можно рассчитать, если базой сравнения является не общий итог, а какая-то одна часть совокупности, по отношению к которой определяются доли других частей совокупности. Относительные величины координации численности рабочих с руководителями, специалистами и служащими по данным табл.2, показывают, что в базисном периоде на 100 рабочих фирмы приходилось 74 человек руководителей, специалистов и служащих (64:86 х 100), а в отчетном уже 67 человек (44:66 х 100).

Относительные величины интенсивности получают путем сравнения объемов разных совокупностей, находящихся в определенной связи друг с другом. Например, выпуск товарной продукции и численность, территория и население. Сравнивая эти совокупности, находим такие относительные величины интенсивности как производительность труда и плотность населения. Разновидностью показателей интенсивности являются показатели экономического развития, такие как душевой доход, производство и потребление различных видов продукции на душу населения и др.

Для характеристики изменения явления во времени применяют относительные величины динамики (темпы). Их вычисляют путем сравнения величины текущего периода к величине одного из прошлых периодов. Если база сравнения постоянная, то темпы динамики базисные, а если переменная, то цепные. Примером расчета базисных и цепных относительных величин динамики является табл. 3.

Таблица 3

Динамика фонда оплаты труда на строительном предприятии

Месяцы	Фонд оплаты труда
тыс. руб.	в % к январю (базисные темпы динамики)	в % к предыдущему месяцу (цепные темпы динамики)
Январь Февраль Март Апрель Май Июнь		—	—

Из таблицы видно, что фонд оплаты труда на предприятии за пять месяцев увеличился на 59% или в 1,59 раза. Цепные темпы показывают, что в каждом месяце по сравнению с предыдущим происходило увеличение фонда оплаты труда. Резкое увеличение фонда заработной платы на 47% произошло в феврале по сравнению с январем.

Относительные величины сравнения представляют собой отношение одноименных величин, характеризующих разные объекты. Так, например, можно сравнить урожайность зерновых культур, среднюю заработную плату, объем промышленной продукции по странам, отдельным регионам и областям. В качестве примера приведем таблицу 4, которая показывает, во сколько раз средняя заработная плата промышленно-производственного персонала в топливной промышленности превышала среднюю заработную плату в других отраслях.

Таблица 4

Среднемесячная заработная плата промышленно-производственного персонала в некоторых отраслях промышленности в 1995 г. *

Отрасль промышленности	Средняя заработная плата ППП, руб.	Отношение средней ЗП ППП в топливной промышленности к средней ЗП в других отраслях
Топливная Электроэнергетика Пищевая Химическая Лесная Легкая	1210 351 985 846 556 709 508 294 450 586 265 583	— 1,2 2,2 2,4 2,7 4,6
* Промышленность России. Госкомстат РФ, 1996. стр.87.

2.4 Средние величины

Статистика изучает массовые явления и процессы. Каждое из таких явлений обладает общими для всей совокупности и индивидуальными свойствами. Различие между индивидуальными свойствами называется вариацией, а присущая массовым явлениям близость (похожесть) характеристик отдельных явлений определяется средними величинами. Наиболее часто в статистике применяется средняя арифметическая, реже — средняя гармоническая, средняя геометрическая применяется только при исчислении средних темпов динамики (см. формулы 5 и 6).

Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных единиц. Например, общий фонд заработной платы состоит из зарплат, начисленных отдельным работникам. Когда имеются отдельные несгруппированные значения признака рассчитывается средняя арифметическая простая по формуле:

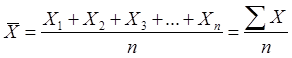, (5)

где X₁, X₂, X₃, …, X_n — индивидуальные значения признака, которые называют вариантами, n— число единиц совокупности.

По данным, представленным в виде рядов распределения или группировок рассчитывается средняя арифметическая взвешенная. Формула для расчета средней арифметической взвешенной имеет вид:

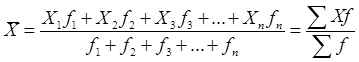, (6)

где X₁, X₂, X₃, …, X_n — варианты. F₁, f₂, f₃, …, f_n – веса или частоты (т.е.-число вариант, имеющих одинаковое значение признака).

Рассмотрим пример расчета средней арифметической взвешенной на основе интервального вариационного ряда.

Таблица 5

Расчет средней заработной платы из вариационного ряда

Группы рабочих по размеру месячной заработной платы, руб.	Среднее значение интервалов (Х)	Число рабочих (f)	Произведение вариант на частоты(X f)
1500-2000 2000-2500 2500-3000
Итого

По данным табл.5 средняя месячная зарплата рабочих составит:

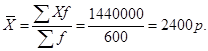
Средняя гармоническая — это величина, обратная средней арифметической, из обратных значений признака. Ее применяют тогда, когда веса приходится не умножать, а делить на варианты или умножать на обратное их значение. Формулы средней гармонической простой и взвешенной имеют вид:

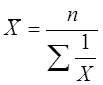, (7)

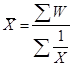, (8)

где n — число единиц совокупности, Х— варианты, W = Xf. Расчет средней гармонической поясним на примере.

Таблица 6

Стоимость продукции и ее выработка в рабочих бригадах

Номер бригады	Стоимость произведенной продукции, тыс. руб. (W = Xf)	Выработка на 1-го рабочего, тыс. руб. (X)
		2,1 2,6 2,9
Итого

Варьирующим признаком в данном примере является средняя выработка рабочих в каждой бригаде. Среднее значение данного варьирующего признака равно 2,4 тыс. руб. Эта средняя получается как средняя гармоническая, где веса деленные на варианты показывают численность рабочих в бригадах, т.е.

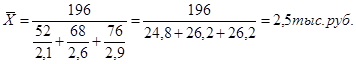
Средне арифметические и средне гармонические величини взаимозаменяемы. Это обусловлено одной и той же логической формулой для искомого показателя. Но вместе с тем данные, по которым могут быть вычислены эти величины, должны быть различными.

Логическая формула вытекает из сущности средней, ее социально-экономического содержания. Поэтому, прежде чем оперировать цифрами, нужно выяснить, соотнашением каких показателей является средняя в данном конкретном случае. Это исходное соотнашение необходимо записать в виде формулы, называемой логической формулой средней. Рассмотрим на примере порядок расчета и выбор формулы средней величины.

Пример. На основании следующих данных по двум сельскохозяйственным предприятиям необходимо определить, в каком из них и насколько выше средняя урожайность зерновых культур:

Культура	Предприятие 1	Предприятие 2
Валовой сбор, ц	Урожайность ц./г	Посевная площадь, га	Урожайность, Ц./г
Пшеница озимая Рожь Ячмень Просо
Итого		-		-

Показатель урожайности является вторичным признаком, так как на единицу первичного признака (посевной площади, выраженной абсолютной величиной) и может быть представлен как отношение двух первычны признаков, а именно валового сбора и посевной площади:

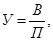
где У-урожайность; В-воловой сбор; П-посевная площадь.

Из выражения (12) вытекает следующая логическая формула:

Следовательно, для расчета средней урожайности по каждому предприятию необходимо применить среднюю взвешенную. Возникает вопрос: арифметическую или гармоническую? В.Е. Овсиенко формализовал порядок выбора вида средней качественного признака на основе следующих правил.

1. Если имеется ряд данных по двум взаимосвязанным показателям, для одного из которых нужно вычислить среднюю величину, и при этом известны численные значения знаменателя ее логической формулы, а значения числителя не известны, но могут быть найдены как произведения этих показателей, то средняя должна вычисляться по формуле средней арифметической взвешенной.

2. Если в указанной постановке задачи известны численные значения числителя логической формулы, а значения знаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя вычисляется по формуле средней гармонической взвешенной.

3. В том случае, когда в условии задачи даны численные значения числителя и знаменателя логической формулы показателя, средняя вычисляется непосредственно по этой формуле.

Согласно данным рассматриваемого примера, для сельскохозяйственного предприятия 1 средняя урожайность должна определяться по правилу 2, изложенному выше, т.е. по формуле средней гармонической взвешенной:

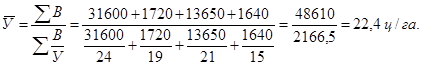
Для сельскохозяйственного предприятия № 2 средняя урожайность определяется по правилу 1, т. е. По формуле средней арифметической взвещенной:

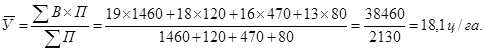
Следовательно, средняя урожайность зерновых культур на предприятии № 1 по сравнению с предприятием № 2 была выше на 4,1 ц/га.

Другими видами средних величин являются структурные средние — мода и медиана.

Модой называется величина признака (варианта), которая чаще всего встречается в совокупности.

В дискретном вариационном ряду модой является варианта, имеющая наибольшую частоту. В интервальном вариационном ряду мода находится внутри модального интервала, который имеет наибольшую частоту и определяется по формуле:

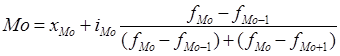, (9)

где Mo — мода, X_Mo — начальное значение интервала, содержащего моду, i_Mo — величина модального интервала, f_Mo — частота модального интервала, f_Mo-1 — частота интервала, предшествующего модальному, f_Mo+1— частота интервала, следующего за модальным.

Медианой называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд на две равные части — со значением признака меньше медианы и со значением признака больше медианы. В дискретном вариационном ряду медианой следует считать значения признака в той группе, где накопленная частота превышает половину объема ряда. В интервальном вариационном ряду медиана находится в медианном интервале, которому соответствует накопленная частота, равная половине общей суммы частот или превышающая эту сумму, и определяется по формуле:

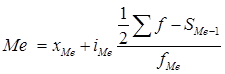, (10)

где Me — медиана,

X_Me — начальное значение интервала, содержащего медиану, i_Me — величина медианного интервала, åf— сумма частот ряда, S_Me-1 — сумма накопленных частот, предшествующих медианному интервалу, f_Me — частота медианного интервала.

Дополнительно к медиане для характеристики структуры вариационного ряда исчисляют квартили, которые делят ряд по сумме частот на 4 равные части. Второй квартиль равен медиане, а первый и третий исчисляются аналогично расчету медианы, только для первого квартиля (Q₁) берется интервал, в котором находится варианта, отсекающая 1/4 суммы накопленных частот, а для третьего квартиля (Q₃)берется интервал, содержащий варианту, отсекающую 3/4 суммы накопленных частот. Формулы расчета первого и третьего квартилей будут иметь вид:

, (11)

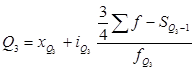, (12)

Приведем пример расчета моды, медианы и квартилей по данным табл.7.

Таблица 7

Распределение предприятий района по сумме прибыли

Прибыль, тыс.руб.	Количество предприятий, f	Накопленные частоты, S
До 50 50-100 100-200 150 – 200 200 – 250 250 - 300 Свыше 300
Итого

В нашем примере модальный и медианный интервалы совпадают.

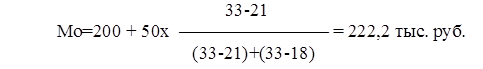
Следовательно, в районе преобладают предприятия, получающие прибыль в размере 222 тыс. руб.

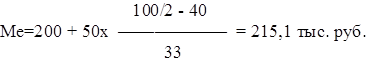
Это значит, что половина всех предприятий района имеет прибыль меньше 215 тыс.руб., а другая половина больше 215 тыс.руб.

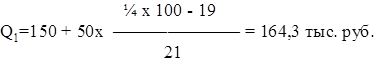
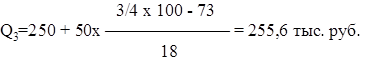
Расчет квартилей показывает, что 25% всех предприятий района поручают прибыль до 164 тыс.руб., другая четверть предприятий имеет прибыль от 164 до 512 тыс.руб., третья четверть — от 512 до 256 тыс. руб., а остальные 25% — свыше 256 тыс.руб.

2.5 Показатели вариации

Исследование вариации в статистике и социально – экономических исследованиях имеет важное значение, так как величина вариации признака статистической совокупности характеризует её однородность.

В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относится размах вариации, среднее линейное отклонение, средний квадрат отклонений (дисперсия), среднее квадратическое отклонение и коэффициент вариации.

Способы вычисления показателей вариации. Размах вариации (R) является наиболее простым измерителем вариации признака.

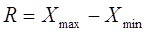, (13)

где 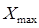- наибольшее значение варьирующего признака;

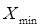- наименьшее значение признака.

Среднее линейное отклонение (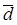) представляет собой среднюю величину из отклонений вариантов признака от средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или частот в ряду распределения:

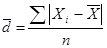- невзвешенное среднее линейное отклонение;

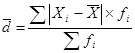- взвешенное средние линейное отклонение.

Символы 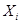, , 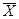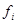и n имеют то же значение, что и в предыдущих параграфах. Рассмотренные выше показатели имеют те же размерность, что и признак, для которого они вычисляются.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины (обозначается греческой буквой 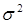- «сигма квадрат»).

Дисперсия вычисляется по формулам простой и не взвешенной и взвешенной:

- не взвешенная;

- взвешенная.

Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней:

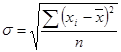- не взвешенное;

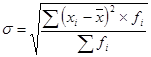- взвешенное.

Среднее квадратическое отклонение – величина именованная, имеет размерность усредняемого признака.

Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

Различают следующие относительные показатели вариации (V):

Коэффициент осцилляции: ,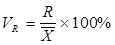

Линейный коэффициент вариации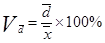

Коэффициент вариации: .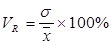

Наиболее часто в практических расчётах из этих трёх показателей применяется коэффициент вариации.

Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяются совокупности, а так же и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Правило сложения дисперсий. Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обуславливающих эту вариацию:

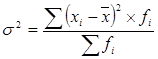, (14)

Межгрупповая дисперсия характеризует систематическую вариацию, т.е., различия в величине изучаемого признака – фактора положенного в основании группировки.

Она рассчитывается по формуле:

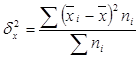(15)

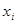где и 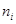- соответственно средние и численности по отдельным группам.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака фактора, положенного в основание группировки.

Она исчисляется следующим образом:

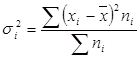(16)

Средняя из внутригрупповых дисперсий:

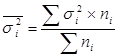, (17)

Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме из внутригрупповых и межгрупповых дисперсий:

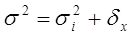, (18)

Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счёт группировочного признака.

Зная любые виды дисперсий, можно определить или проверить правильность расчёта третьего вида.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Она называется эмпирическим корреляционным отношением, обозначается («эта») и рассчитывается по формуле:

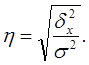(19)

Тесты

1. Способами статистического наблюдения не являются:

а) непосредственное;

б) саморегистрация;

в) экспедиционный способ;

г) выборочное.

2. Видами статистического наблюдения не являются:

а) по признаку характера учета факторов во времени;

б) по признаку, характеризующему объект наблюдения;

в) по признаку полноты охвата совокупности.

3. Сводкой в статистическом анализе называется:

а) объединенние единиц совокупности в некоторые группы, имеющие свои харакерные особенности, общие черты и сходные размеры изучаемого признака;

б) объект, характеризующийся цифрами;

в) это научно организованная обработка материалов наблюдения, включающая в себя систематизацию, группировку данных,составление таблиц, подсчет групповых и общих итогов,расчет производных показателей.

4. Для измерения вариации значения признака не вычисляют показатели:

а) моду;

б) дисперсию;

в) размах вариации;

г) среднелинейное отклонение;

д) коэффициент вариации.

5.Модой в статистике называют:

а) значение признака, которое чаще всего встречается в данной совокупности;

б) знчение пизнака у единицы, которое находится в середине упорядоченного ряда распределения;

в) значение признака, которое встречается в данной совокупности единственный раз.

6.Если данные сгруппированы, но каждое значение признака встречается неодинаковое количество раз, то применяется формула (запишите ее):

а) средняя гармоническая простая;

б) средяя хронологическая;

в) средняя арифметическая взвешенная;

г) средняя гармоническая взвешенная.

7.Ряды распределения называют вариационными:

а) построенные по количественному призку;

б) построенные по качественному признаку;

в) построенные в порядке убывания.

8.Под ранжированием понимаются:

а) определение предела значений варьирующего признака;

б) определение среднелинейного отклонения;

в) разложение всех вариантов пизнака возрастающем (или убывающем) порядке.

Тема 3. Статистическое изучение динамики социально-экономических явлений

Введение

Данная глава знакомит студентов с задачами, решение которых даёт возможность усвоить правила построения и анализа рядов динамики для характеристики изменения социально-экономических явлений во времени, выявления основной тенденции, закономерности их развития. Достигается это соответствующей обработкой рядов динамики, анализом изменения его уровней, расчетом аналитических показателей. Это важный раздел курса теории статистики, так как в большинстве случаев задачей статистического исследования бывает анализ развития тех или иных явлений.

Цели

В результате изучения этой главы вы сможете:

- анализировать динамику показателей;

- определять тенденцию изменения показателей;

- строить прогнозные значения показателей.

3.1 Виды рядов динамики. Показатель динамики.

Начиная изучение темы, необходимо обратить внимание на классификацию рядов динамики, различия между ними, так как отнесение ряда динамики к тому или иному виду имеет важное значение для их изучения. Выбор соответствующих приёмов и способов анализа определяется характером исходных данных и зависит от задач исследования.

В зависимости от способа выражения уровней (в виде абсолютных, относительных исреднихвеличин) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. В зависимости от того, выражают уровни ряда состояние явления на определенный момент времени (на начало месяца, квартала года и т.п.) или его величину за определённый интервал времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды. Ряды динамики могут быть с равноотстоящими (по времени) уровнями и не равноотстоящими (по времени) уровнями.