2015-04-01
294
Покажем на примерах как наличие информации влияет на выбор решения и соответственно на ожидаемый результат.
Пример 1: Информация о выборе партнера
Рассмотрим антагонистическую игру: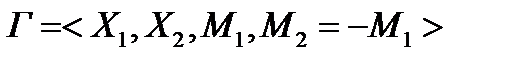 
.
Пусть первый игрок не имеет информации о выборе второго игрока х2 до своего выбора управления х1.
Тогда его оптимальный (максимально гарантированный результат – МГР) равен:
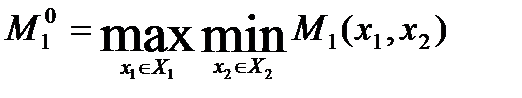
Пусть теперь первый игрок будет иметь информацию о выборе 
вторым игроком.
Тогда игрок 1 может использовать абсолютно оптимальную стратегию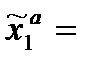 
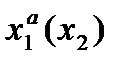, такую что 
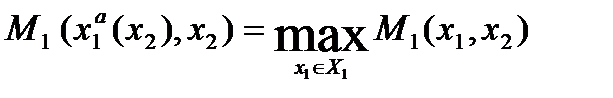при любых 
.
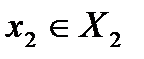В этом случае оптимальный (МГР) результат игрока1 равен:
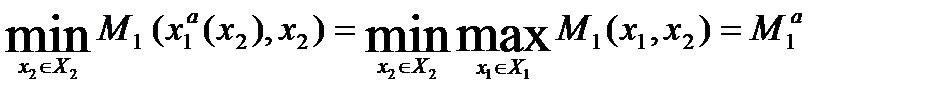
Всегда верно неравенство: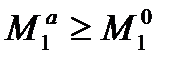 
,
.
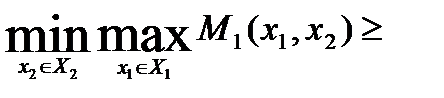
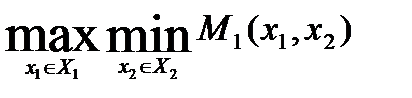Приведем пример когда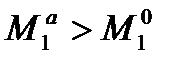 
:
Пусть функция выигрыша первого игрока имеет вид: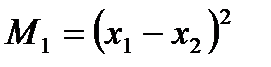 
, 
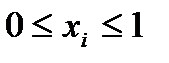, i=1,2
В этом случае, не имея информации о выборе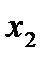 
игрок 1 (ожидая выбора 
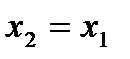) может рассчитывать только на глобальный минимум: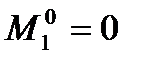 
Пусть теперь игрок 1 будет знать 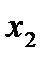до выбора 
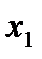. Построим абсолютно оптимальную стратегию игрока 1:
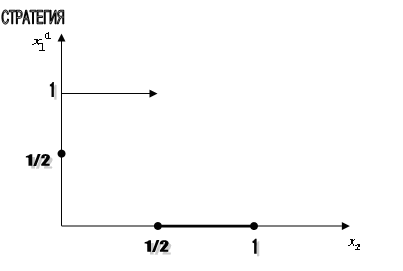
Рис.1.
Итак,
= 
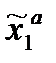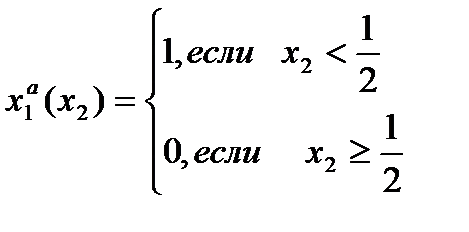
Функция
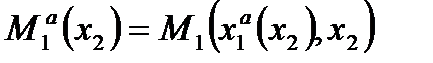имеет вид (см. рис. 2):
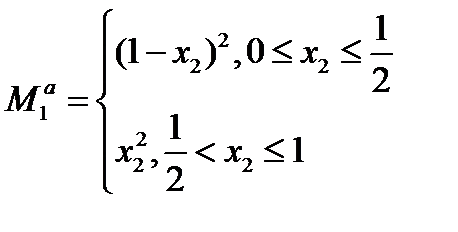
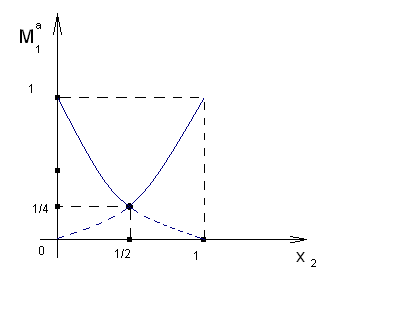
Рис.2.
Тогда оптимальный ответ второго игрока:
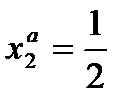
Что дает первому игроку:
= 
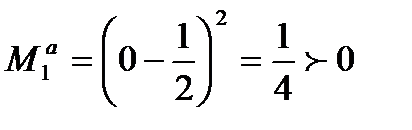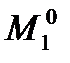
Таким образом, получение своевременной информации о выборе партнера (противника) может дать ощутимый выигрыш.
Пример 2: Роль информации о правиле поведения (о принципе оптимальности) партнера.
Рассмотрим игру: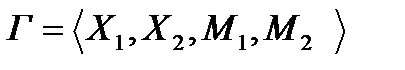 
. Предположим, что первый игрок знает, что игрок 2 осторожен, т.е. придерживается принципа максимального гарантированного результата, а, следовательно, выбирает 
из множества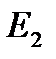 
:
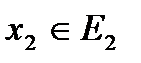, если
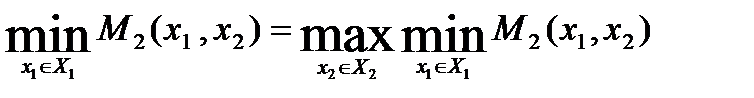
Заметим, что осторожность игрока 2 может обуславливаться отсутствием у него информации о правиле поведения (функции выигрыша) игрока 1.
Итак, если игрок 1 не знает правило поведения игрока 2, то его оптимальный (МГР) результат равен:
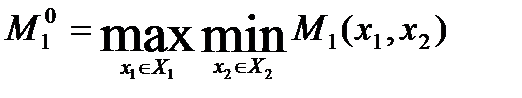
Если же игрок 1 знает отмеченное выше правило поведения игрока 2, то его оптимальный выигрыш оценивается величиной:
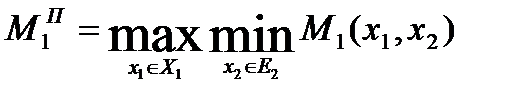
Так как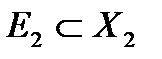 
, то всегда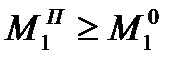 
Замечание: Знать правило поведения (принцип оптимальности) это значит знать функцию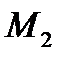 
, множество 
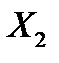и принцип выбора (в данном случае МГР).
Покажем, что возможно строгое неравенство 
.
Пусть, например, функции выигрышей имеют вид:
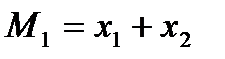
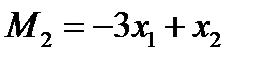
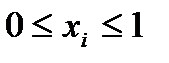, i=1,2
Тогда имеем:
,
,
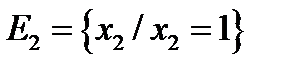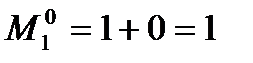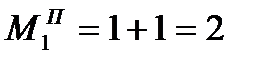
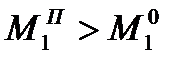
Итак, дополнительная информация – информация о правиле поведения партнера дает дополнительный выигрыш.
Замечание: При моделировании конфликтных ситуаций всегда нужно фиксировать информированность, например, игрока 1 о параметрах модели, описывающих игрока 2: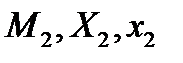 
и т.д.
