Информационное расширение игры

Пусть задана исходная игра Г=<X₁, X₂, M₁, M₂>, тогда игра

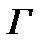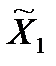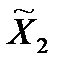
I=<X1,X2,π,M1(x1,x2),M2(x1,x2)называется информационным расширением игры , если существует проекция π: × 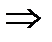X₁×X_2, обладающая следующими свойствами:

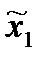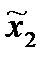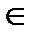
1) Каждой паре стратегий (, ) 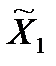× 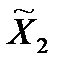ставит в соответствие пару управлений (исходов) (x₁, x₂) 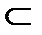X₁×X_2, т.е. (x1, x2) ---->(x 1,x 2)

2) Множество стратегий 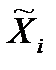содержит стратегии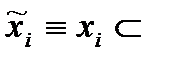 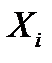, т.е. стратегии – управления, не использующие информации.

3) Функции выигрыша в игре 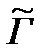вычисляются по правилу:

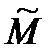_i(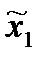, 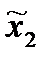) = M_i(π (, ))

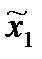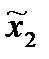Не для любых множеств стратегий выполняется свойство (1), а следовательно и свойства (2) и (3).

Например, возьмем пару { 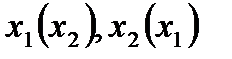}. В этом случае игрок 1 знает о выборе второго, а игрок 2 одновременно знает выбор первого - противоречие. Следовательно, пара { 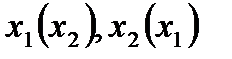} «физически» не реализуема.

Свойство (2) заключается в следующем:

Игроки могут использовать стратегии, для выбора которых не требуется учета информации, но это, как правило, нецелесообразно (приводит к потере выигрыша).

Выигрыши в игре 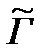определяются по свойству (3) равенством:

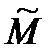_i(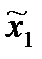, 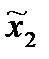) = M_i(π (, ))

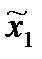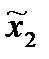Т.е. сначала стратегии (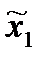, 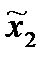) проектируются во множество управлений (исходов) - (x₁, x₂) 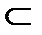X₁×X₂, а затем вычисляются значения 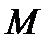_i(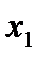, 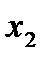), как и в игре Г.