В этой игре существует единственная ситуация равновесия – обоим партнерам рекламировать свой товар. Однако существует более эффективный для обоих партнеров вариант, оптимальный по Парето, - не тратиться на рекламу. Но эта ситуация не является равновесной на классе исходных управлений. Однако эта ситуация принадлежит взаимовыгодному множеству, а значит ее можно сделать результатом проекции равновесных стратегий, включающих в себя договорные обязательства со штрафами за отклонение от них.
Пример. [1]
Пусть биматричная игра имеет вид:
М1= 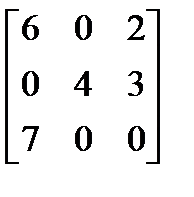 M2=
M2= 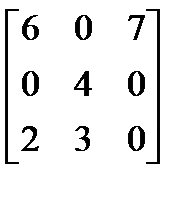
Исследуем множество равновесных ситуаций в этой игре.
Имеем для игрока 1:
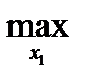
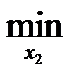 M1(x1, x2) = 0
M1(x1, x2) = 0
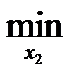
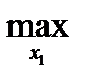 M1(x1, x2) = 3
M1(x1, x2) = 3
Определим: х2 = х2H - стратегия наказания первого игрока вторым, из условия 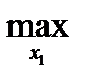
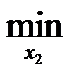 M1(х1, х2) =
M1(х1, х2) = 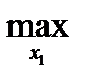 M1(х1, х2H) В данном случае имеем х2H=
M1(х1, х2H) В данном случае имеем х2H= 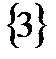 .
.
Далее для игрока 2 имеем: 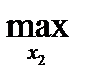
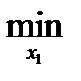 M2(x1, x2) = 0
M2(x1, x2) = 0
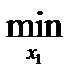
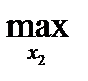 M2(x1, x2) = 3
M2(x1, x2) = 3
Определим х1H (х2) - стратегию наказания второго игрока первым.
2, если х1 = 1
х1H (х2)= 1, если х2 = 2
3 (2), если х3 =3
Сначала найдем равновесные ситуации в исходной игре.
Для этого определим:
|
|
|
x1a(x2) –абсолютно оптимальную стратегию первого игрока и
х2 = x2a – оптимальный ответ второго.
Напомним, что:
x1a(x2): M1(x1a(x2), x2) = 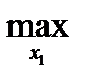 M1(x1, x2)x2a:
M1(x1, x2)x2a:
M2(x1a(x2а), x2a) = 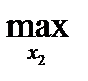 M2(x1a(x2а), x2).
M2(x1a(x2а), x2).
Итак:
3, если x2 = 1
x1a(x2) = 2, если x2 = 2
2, если x2 = 3
Аналогично: 3, если x1 = 1
x2a(x1) = 2, если x1 = 2
2, если x1 = 3
Единственная ситуация равновесия в исходной игре определяется из условия
x1a(x2а) = x2a(x1a)  (2,2).
(2,2).
В этой ситуации выигрыши игроков равны (4,4).
Замечание.
Прием построения абсолютно оптимальных стратегий и нахождения их пересечений для определения ситуаций равновесия носит общий характер.
Построим П-множество Парето на классе исходных управлений.
Напомним, что
(x1п, x2п)  П
П
если не существует (x1', x2')єХ1*Х2, такой что:
Mi(x1', x2') ≥ Mi(x1п, x2п), i=1, 2 (дизъюнкция)
Mi(x1', x2') > Mi(x1п, x2п), i=1 либо i=2 (конъюнкция)
В пространстве выигрышей множество возможных решений имеет вид:
M2
П
7
6 П
4 (4, 4) с.р.
2 П
0 2 3 4 6 7 M1
рис.1
Как видно из рис.1:
П = {(1,1); (1,3); (3,1)},
С выигрышами игроков соответственно
МП = {(6,6); (2,7); (7,2)}.
Непосредственной проверкой убеждаемся, что ни одна из этих точек не является ситуацией равновесия в исходной игре.
Покажем, что эти ситуации могут быть результатом проекции равновесных стратегий вида:
{ х1(х2), х2[х1(х2)]}, {х1[х2(х1)], х2(х1)}.
Покажем, что равновесные стратегии можно выбрать на классе стратегий {x1(x2), x2 [x1(x2)]}.Действительно, пусть
x10 (x2) = 1, х2=1 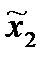 0 = х20 [х1(х2)] = 1,
0 = х20 [х1(х2)] = 1, 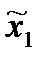 =
= 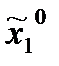
х1н (х2), х2 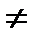 1, х2н = 3,
1, х2н = 3, 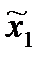
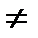
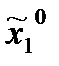
Очевидно, эти стратегии проектируются в точку (х1 = 1, х2=1). В этой точке M1 = 6, M2 = 6.
Если от этих стратегий отклонится игрок 1, то есть 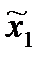
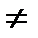
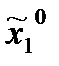 , то он получит не больше, чем
, то он получит не больше, чем
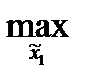 M1(π(
M1(π(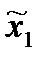 ,
, 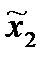 0))=
0))= 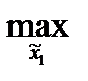 M1(π (
M1(π (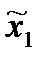 , 3) = M1(2, 3) = 3 < 6.
, 3) = M1(2, 3) = 3 < 6.
Таким образом, игроку 1 не выгодно отклоняться от точки (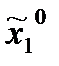 ,
, 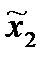 0).
0).
|
|
|
Если же при 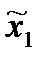 =
= 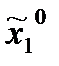 , игрок 2 выберет
, игрок 2 выберет 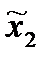
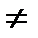
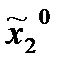 , то его выигрыш оценивается величиной
, то его выигрыш оценивается величиной
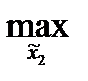 M2[π(
M2[π(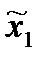 0,
0, 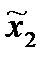 )].
)].
Если 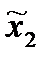 т.ч. х2
т.ч. х2 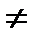 1, при
1, при 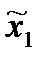 =
= 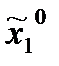 , то
, то
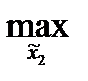 M2[π(
M2[π(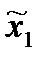 0,
0, 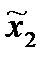 )] =
)] = 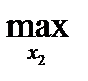 M2(х1H(х2), х2) = 0 < 6
M2(х1H(х2), х2) = 0 < 6
Итак, игроку 2 также не выгодно отклоняться от точки (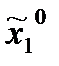 ,
, 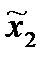 0), то есть (
0), то есть (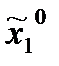 ,
, 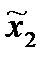 0) – ситуация равновесия в игре
0) – ситуация равновесия в игре 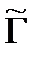 .
.
Упражнение.
Точку (7,2) можно сделать ситуацией равновесия на классе
{x1(x2), x2 [x1(x2)]}
Точку (2,7) можно сделать ситуацией равновесия на классе
{x2(x1), x1 [x2(x1)]}.
Замечание.
Точку из множества Парето можно сделать равновесной, если выигрыши игроков в ней оцениваются величиной не меньшей, чем их максимально гарантированные результаты, соответствующие их информированности. Этому условию удовлетворяет точка (7,2) на классе стратегий {x1(x2), x2 [x1(x2)]} и точка (2,7) на классе стратегий {x2(x1), x1 [x2(x1)]}.
Примеры на стратегиях!!!
 2015-04-01
2015-04-01 314
314








