Примеры 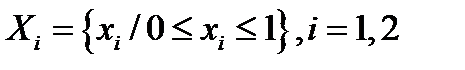проектирования множества стратегий на множество управлений (выборов, исходов)

Пример 1:

Пусть 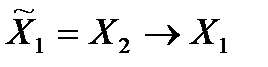, т.е. ,

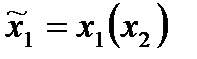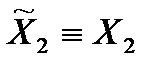, т.е.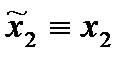

Тогда (, ) .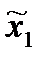

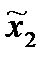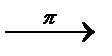
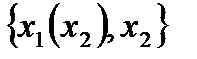Фиксируем для примера:

X1=x(x2)=x2^2

X2=x2=1/2.

Тогда эти стратегии проектируются так:

(x 1, x 2)à (x 1 (x 2), x 2)à (x 2/2, ½) =(1/4,1/2)

Пример 2: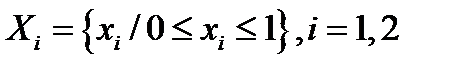

Пусть x1: x 2 à X 1 т.е. ,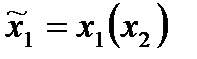

x 2: x 1àX 2, т.е. 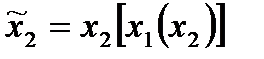- игрок 2 принимает решение в зависимости от стратегии первого игрока. Например,

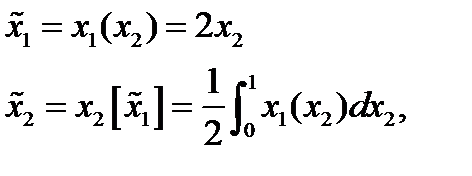
Проектируем:

,

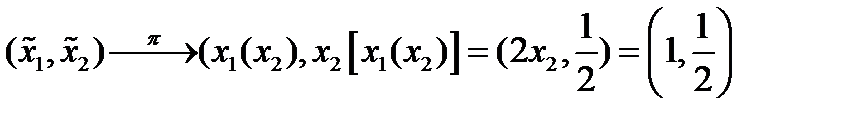так как

.

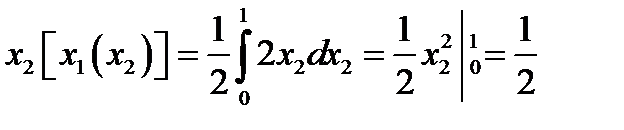Полезные свойства стратегий:

1) На классе стратегий ситуация равновесия по Нэшу существует всегда, необходимо только организовать соответствующий обмен информацией.

2) На классе стратегий из примера 2 можно сделать равновесной любую взаимовыгодную точку. Взаимовыгодное множество – это множество, где игроки получают больше своих максимально гарантированных результатов, следовательно, паретовскую точку можно сделать равновесной.