Пусть задана игра:
Г = <  ,
,  ,
,  ,
,  >
>
и ее информационное расширение:
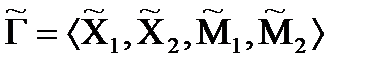

Определение.
(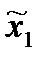 0,
0, 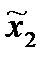 0)- ситуация равновесия в информационном расширении игры, если M10 =M1(π(
0)- ситуация равновесия в информационном расширении игры, если M10 =M1(π(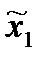 0,
0, 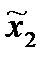 0))=
0))= 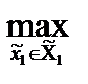 M1(π(
M1(π(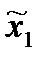 ,
, 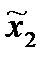 0))
0))
M20= M2(π(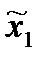 0,
0, 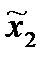 0))=
0))= 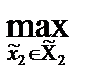 M2(π(
M2(π(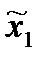 0,
0, 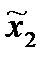 )
)
Заметим,что
(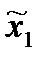 0,
0, 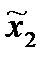 0) π (х10, х20) – равновесный исход, но не ситуация равновесия!
0) π (х10, х20) – равновесный исход, но не ситуация равновесия!
Таким образом, ситуация равновесия может реализоваться на стратегиях
(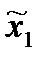 º,
º, 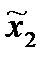 º) є
º) є 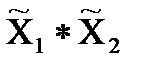
но ее проекция
(хº1, хº2) є 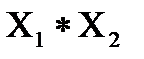
не обязательно равновесная по Нэшу.
Напомним, что стратегия 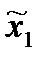 а = х1а(х2) называется абсолютно оптимальной стратегией, если справедливо равенство:
а = х1а(х2) называется абсолютно оптимальной стратегией, если справедливо равенство:
M1(x1а(x2), x2)= 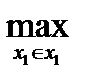 M1(x1, x2)
M1(x1, x2)
Определим x2= х2а - оптимальный ответ второго игрока из условия:
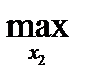 M2(x1а(x2), x2) = M2(x1а(x2а), x2а)
M2(x1а(x2), x2) = M2(x1а(x2а), x2а)
Положительные свойства стратегий:
Свойство 1.
Ситуация равновесия всегда существует на классе стратегий
(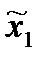 ,
, 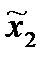 )=(x1(x2), x2)
)=(x1(x2), x2)
Доказательство: Достаточно выбрать абсолютно оптимальную стратегию 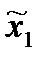 а = хª1(x2), и оптимальный ответ на нее
а = хª1(x2), и оптимальный ответ на нее 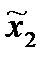 а = х2а
а = х2а
По определению:
M1(x1а(x2), x2) = 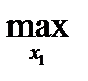 M1(x1, x2),
M1(x1, x2),
M2(x1а(x2а), x2а) = 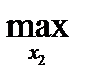 M2(x1а(x2), x2).
M2(x1а(x2), x2).
Тогда, если 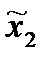 = х2а, то
= х2а, то
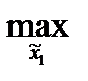 M1(π(
M1(π(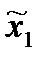 ,x^2а))=
,x^2а))= 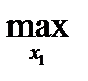 M1(x1(xª2), xª2) = M1(x1а(x2а), x2а).
M1(x1(xª2), xª2) = M1(x1а(x2а), x2а).
Если 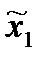 =
= 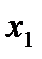 а (
а (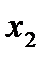 ), то
), то 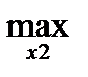 M2(x1а(x2), x2)= M2(x1а(x2а), x2а), что соответствует определению ситуации равновесия в информационном расширении игры.
M2(x1а(x2), x2)= M2(x1а(x2а), x2а), что соответствует определению ситуации равновесия в информационном расширении игры.
Свойство 2.
Если 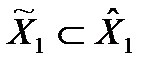 , то и
, то и 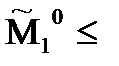
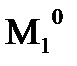
 – увеличение информации приводит к возможности увеличения выигрыша.т
– увеличение информации приводит к возможности увеличения выигрыша.т
Доказательство:
Первый игрок может не использовать дополнительную информацию и получить 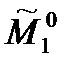 . А если повезёт (дополнительная информация оказалась полезной), то получит строго больше.
. А если повезёт (дополнительная информация оказалась полезной), то получит строго больше.
Свойство 3.
Пусть игрок 1 знает х2.
Определим взаимовыгодное множество для этого случая:
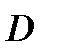 12={(х1, х2)
12={(х1, х2) 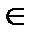
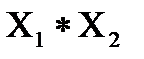 M1(х1, х2) ≥
M1(х1, х2) ≥ 
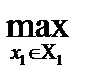 M1(х1, х2);
M1(х1, х2);
M2(х1, х2) ≥ 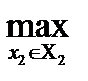
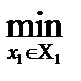 M2(х1, х2)}.
M2(х1, х2)}.
Любая точка из этого множества может быть сделана ситуацией равновесия на классе стратегий
{х1(х2), х2[х1(х2)]}
Аналогичное утверждение верно и в симметричном случае, когда игрок 2 знает х1.
Здесь взаимовыгодное множество имеет вид:
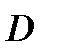 21={(х1, х2)
21={(х1, х2) 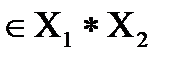 M1(х1, х2) ≥
M1(х1, х2) ≥ 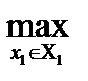
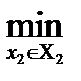 M1(х1, х2);
M1(х1, х2);
M2(х1, х2) ≥ 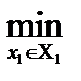
 M2(х1, х2)}.
M2(х1, х2)}.
А класс использованных стратегий имеет вид:
{ х1 [х2(х1)], х2 (х1)}.
ТРИ игры
Проведем анализ рассмотренных ранее игр,но уже на классе стратегий.
 2015-04-01
2015-04-01 324
324








