Исходные данные к разделу 2

Вариант № 1. Однопараметрическое показательное распределение:

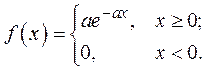
Исходные данные: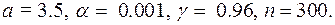

Рассчитать аналитически: .

Найти точечную оценку параметра 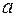методом моментов.

Вариант № 2. Общее показательное распределение:

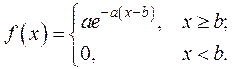
Исходные данные:

Рассчитать аналитически: .

Найти точечные оценки параметров 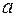и 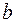методом моментов.

Вариант № 3. Однопараметрическое распределение Лапласа:

.

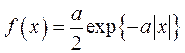Исходные данные: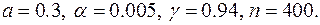

Рассчитать аналитически: .

Найти точечную оценку параметра 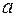методом моментов.

Вариант № 4. Общее распределение Лапласа:

.

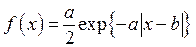Исходные данные: a = 1.5, b = -2, a = 0.005, g = 0.94, n = 350.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 5. Распределение Релея:

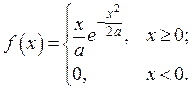
Исходные данные: a = 4, a = 0.025, g = 0.999, n = 375.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 6. Однопараметрическое логистическое распределение:

.

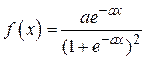Исходные данные: a = 1/2, a = 0.025, g = 0.9, n = 400.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 7. Общее логистическое распределение:

.

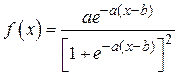Исходные данные: a = 1/2, b = 3, a = 0.025, g = 0.95, n = 350.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 8. Распределение Эрланга k-го порядка:

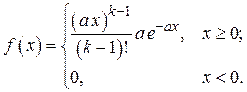
Исходные данные: a = 2, k = 3, a = 0.025, g = 0.9, n = 400.

Рассчитать аналитически: .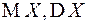

Найти точечные оценки параметров a и k методом моментов.

Указание: Воспользоваться тем, что моделируемая случайная величина

,

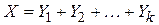где случайные величины 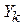- независимы и распределены по показательному закону с параметром a, то есть , .

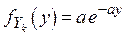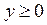Вариант № 9. Степенное распределение:

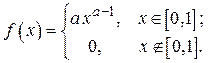
Исходные данные: a = 4, a = 0.05, g = 0.92, 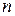= 300.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 10. Степенное распределение:

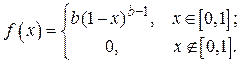
Исходные данные: b = 5, a = 0.05, g = 0.92, 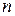= 300.

Рассчитать аналитически: .

Найти точечную оценку параметра b методом моментов.

Вариант № 11. Однопараметрическое распределение прямоугольного треугольника:

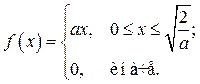
Исходные данные: a = 0.5, a = 0.1, g = 0.98, n = 250.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 12. Однопараметрическое распределение прямоугольного треугольника:

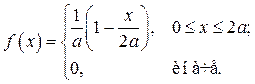
Исходные данные: a = 3, a = 0.1, g = 0.98, n = 250.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 13. Общее распределение прямоугольного треугольника:

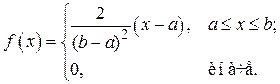
Исходные данные: a = -2, b = 3, a = 0.01, g = 0.95, n = 250.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 14. Однопараметрическое распределение Симпсона: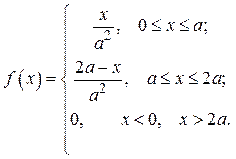

Исходные данные: a = 2, a = 0.05, g = 0.98, n = 300.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 15. Симметричное однопараметрическое распределение Симпсона:

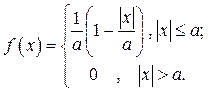
Исходные данные: a = 2, a = 0.05, g = 0.95, n = 300.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 16. Общее распределение Симпсона:

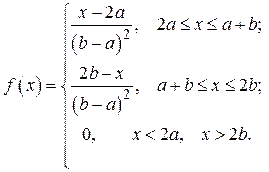
Исходные данные: a = -0.8, b = 0.5, a = 0.05, g = 0.98, n = 300.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 17.

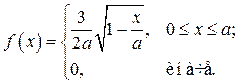
Исходные данные: a = 3, a = 0.1, g = 0.98, n = 350.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 18.

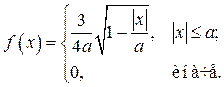
Исходные данные: a = 2, a = 0.1, g = 0.95, n = 350.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 19.

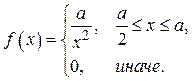
Исходные данные: a = 2, a = 0.1, g = 0.98, n = 250.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 20.

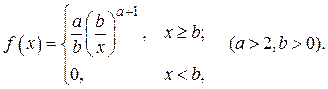
Исходные данные: a = 2, b = 10, a = 0.1, g = 0.98, n = 450.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 21.

.

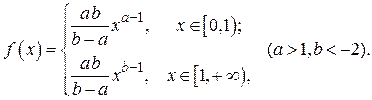Исходные данные: a = 2, b = -3, a = 0.002, g = 0.96, n = 350.

Считая параметр a известным, рассчитать аналитически: 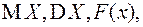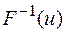. Найти точечную оценку параметра b методом моментов.

Вариант № 22.

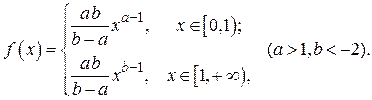
Исходные данные: a = 3, b = -3, a = 0.002, g = 0.98, n = 350.

Считая параметр b известным, рассчитать аналитически: 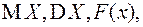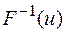. Найти точечную оценку параметра a методом моментов.

Вариант № 23. Распределение арксинуса:

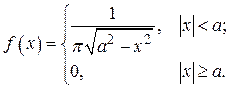
Исходные данные: a = 1/2, a = 0.025, g = 0.94, n = 400.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 24.

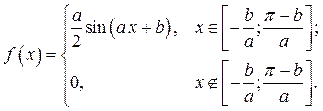
Исходные данные: a = 2, b = 1, a = 0.05, g = 0.98, n = 400.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 25.

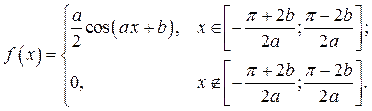
Исходные данные: a = 1.5, b = -1, a = 0.01, g = 0.98, n = 400.

Рассчитать аналитически: .

Найти точечные оценки параметров a и b методом моментов.

Вариант № 26.

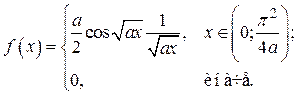
Исходные данные: a = 1/2, a = 0.01, g = 0.96, n = 300.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 27.

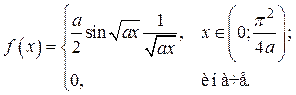
Исходные данные: a = 1/2, a = 0.001, g = 0.95, n = 300.

Рассчитать аналитически: .

Найти точечную оценку параметра a методом моментов.

Вариант № 28. Гамма-распределение:

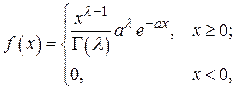
где 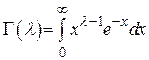- гамма-функция.

Исходные данные: a = 2, l = 3/2, a = 0.01, g = 0.99, n = 400.

Рассчитать аналитически: .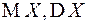

Найти точечные оценки параметров a и l методом моментов.

Указание: Воспользоваться алгоритмом моделирования для случая, когда 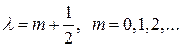или общим алгоритмом моделирования гамма-распределения.

Вариант № 29. Общее бета-распределение:

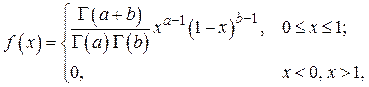
где 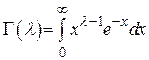- гамма-функция.

Исходные данные: a = 2, b = 2, a = 0.05, g = 0.95, n = 300.

Рассчитать аналитически: .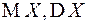

Найти точечные оценки параметров a и b методом моментов.

Указание: Воспользоваться алгоритмом моделирования для случая целых a и b или общим алгоритмом моделирования бета-распределения.

Вариант № 30. Распределение Парето:

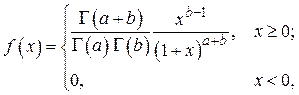
где 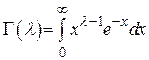- гамма-функция.

Исходные данные: a = 2, b = 2, a = 0.05, g = 0.92, n = 300.

Рассчитать аналитически: .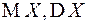

Найти точечные оценки параметров a и b методом моментов.

Указание: Воспользоваться тем, что моделируемая случайная величина 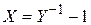, где 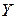- случайная величина, имеющая бета-распределение с параметрами a и b