2.1.1. Записать выборку (5, 3, 7, 10, 5, 5, 2, 10, 7, 2, 7, 7, 4, 2, 4) в виде вариационного ряда и статистического ряда, обозначив 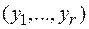 различные среди выборочных значений
различные среди выборочных значений 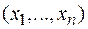 .
.
2.1.2. В эксперименте наблюдалась целочисленная случайная величина 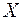 . Соответствующие выборочные значения оказались равными (3, 0, 4, 3, 6, 0, 3, 1). Записать их в виде статистического ряда, найти соответствующую эмпирическую функцию распределения
. Соответствующие выборочные значения оказались равными (3, 0, 4, 3, 6, 0, 3, 1). Записать их в виде статистического ряда, найти соответствующую эмпирическую функцию распределения 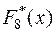 и изобразить ее графически.
и изобразить ее графически.
2.1.3. Пусть (0,8; 2,9; 4,4; -5,6; 1,1; -3.2) – наблюдавшиеся значения некоторой случайной величины. Построить эмпирическую функцию распределения 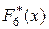 и проверить, что
и проверить, что 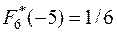 ,
, 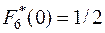 ,
, 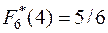 .
.
2.1.4. Найти и изобразить графически эмпирические функции распределения, соответствующие следующим выборкам, представленным в виде статистических рядов:
| а) | 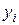 | б) | 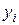 | |||||||
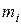 | 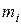 |
2.1.5. Построить эмпирические функции распределения и вычислить выборочные средние и выборочные дисперсии, соответствующие следующим выборкам, представленным в виде статистических рядов:
| а) |
| ||||||||||||
| б) |
|
2.1.6. В результате эксперимента непрерывная случайная величина 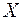 приняла следующие значения (округленные до целых): (6, 17, 9, 13, 21, 11, 7, 7, 19, 5, 17, 5, 20, 18, 11, 4, 6, 22, 21, 15, 15, 23, 19, 25, 1) Построить интервальный статистический ряд, взяв 5 интервалов одинаковой длины; построить гистограмму и полигон частот.
приняла следующие значения (округленные до целых): (6, 17, 9, 13, 21, 11, 7, 7, 19, 5, 17, 5, 20, 18, 11, 4, 6, 22, 21, 15, 15, 23, 19, 25, 1) Построить интервальный статистический ряд, взяв 5 интервалов одинаковой длины; построить гистограмму и полигон частот.
2.1.7. Построить гистограмму и полигон частот по следующим статистическим данным, представленным в виде интервального статистического ряда:
| Номер интервала k | Границы интервала 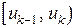 | Частота интервала 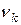 |
| 0 – 2 2 – 4 4 – 6 6 – 8 8 – 10 10 – 12 12 - 14 |
Найти и построить эмпирическую функцию распределения 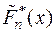 , соответствующую этим сгруппированным данным; вычислить выборочное среднее и выборочную дисперсию.
, соответствующую этим сгруппированным данным; вычислить выборочное среднее и выборочную дисперсию.
2.1.8. Проводились опыты с бросанием 12 игральных костей. Наблюдаемую случайную величину 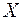 брали равной числу костей, на которых выпало 4, 5 или 6 очков. Пусть
брали равной числу костей, на которых выпало 4, 5 или 6 очков. Пусть 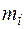 - число опытов, в которых наблюдалось значение
- число опытов, в которых наблюдалось значение 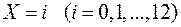 . Ниже приведены результаты
. Ниже приведены результаты 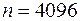 опытов:
опытов:
| i | |||||||||||||
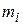 |
Взяв в качестве интервалов 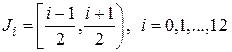 , построить гистограмму и полигон частот. Вычислить выборочное среднее и выборочную дисперсию, соответствующие этим данным.
, построить гистограмму и полигон частот. Вычислить выборочное среднее и выборочную дисперсию, соответствующие этим данным.
2.1.9. Ниже приведены результаты измерения роста случайно отобранных 100 студентов:
| Рост, см | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студентов |
Найти выборочное среднее и выборочную дисперсию роста обследованных студентов, построить гистограмму и полигон частот.
2.1.10. На телефонной станции производились наблюдения за числом неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты:
(3, 1, 3, 4, 2, 1, 1, 3, 2, 7, 2, 0, 2, 4, 0, 3, 0, 2, 0, 1, 3, 3, 1, 2, 2, 0, 2, 1, 4, 3,
4, 2, 0, 2, 3, 1, 3, 1, 4, 2, 2, 1, 2, 5, 1, 1, 0, 1, 1, 2, 1, 0, 3, 4, 1, 2, 2, 1, 1, 5).
Найти выборочное среднее и выборочную дисперсию числа неправильных соединений в минуту и сравнить эмпирическое распределение с распределением Пуассона.
2.1.11. Измерительным прибором, практически не имеющим систематической погрешности, было сделано пять независимых измерений некоторой величины. Получены следующие результаты:
| Номер измерения | |||||
| Результат измерения |
Найти: а) выборочную дисперсию погрешности измерения, если измеряемая величина точно известна и равна 2800; б) выборочное среднее и выборочную дисперсию, если точное значение измеряемой величины неизвестно.
2.1.12. Доказать, что выборочные начальные и выборочные центральные моменты 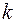 -го порядка связаны соотношением:
-го порядка связаны соотношением:
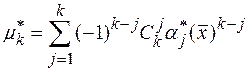 .
.
 2015-04-01
2015-04-01 1445
1445







