2.3.1. Найти доверительный интервал для математического ожидания нормально распределенной случайной величины 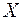 , если известны дисперсия
, если известны дисперсия 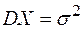 , выборочное среднее
, выборочное среднее 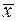 , объем выборки
, объем выборки 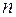 и доверительная вероятность
и доверительная вероятность 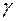 :
:
а) 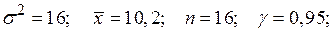
б) 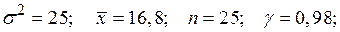
в) 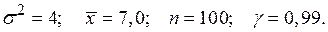
2.3.2. Одним и тем же прибором со средним квадратическим отклонением случайных ошибок измерений 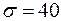 м произведено пять равноточных измерений высоты полета аппарата. Найти доверительный интервал для истинной высоты
м произведено пять равноточных измерений высоты полета аппарата. Найти доверительный интервал для истинной высоты 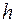 полета с надежностью
полета с надежностью 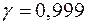 , зная среднее арифметическое результатов измерений
, зная среднее арифметическое результатов измерений 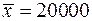 м, и предполагая, что результаты измерений распределены нормально.
м, и предполагая, что результаты измерений распределены нормально.
2.3.3. Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания 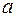 случайной величины
случайной величины 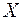 по выборочному среднему равна 0,3, если известна дисперсия
по выборочному среднему равна 0,3, если известна дисперсия 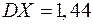 .
.
2.3.4. Построить доверительный интервал для математического ожидания нормально распределенной случайной величины 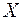 , если известны выборочное среднее
, если известны выборочное среднее 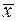 , выборочная дисперсия
, выборочная дисперсия 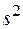 , объем выборки
, объем выборки 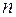 и доверительная вероятность
и доверительная вероятность 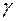 :
:
а) 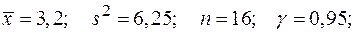
б) 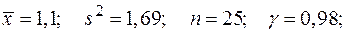
в) 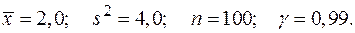
2.3.5. По данным девяти независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений 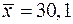 и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение 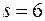 . Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью
. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью 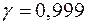 . Предполагается, что результаты измерений распределены нормально.
. Предполагается, что результаты измерений распределены нормально.
2.3.6. Построить доверительный интервал для дисперсии нормально распределенной случайной величины 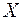 , если известны выборочная дисперсия
, если известны выборочная дисперсия 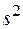 , объем выборки
, объем выборки 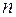 и доверительная вероятность
и доверительная вероятность 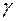 :
:
а) 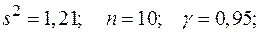 б)
б) 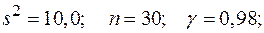
в) 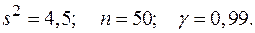
2.3.7. Зная выборочную дисперсию 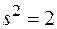 и объем выборки
и объем выборки 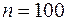 из нормальной генеральной совокупности, построить точный и приближенный доверительные интервалы для неизвестной дисперсии
из нормальной генеральной совокупности, построить точный и приближенный доверительные интервалы для неизвестной дисперсии 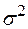 , отвечающие доверительной вероятности
, отвечающие доверительной вероятности 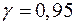 . Сравнить полученные результаты.
. Сравнить полученные результаты.
2.3.8. Построить доверительный интервал для математического ожидания случайной величины 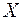 , имеющей биномиальное распределение
, имеющей биномиальное распределение 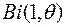 , если выборочное среднее
, если выборочное среднее 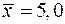 , а объем выборки
, а объем выборки 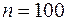 . Доверительную вероятность принять равной
. Доверительную вероятность принять равной 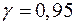 .
.
2.3.9. Зная объем выборки 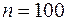 , выборочное среднее
, выборочное среднее 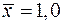 , выборочную дисперсию
, выборочную дисперсию 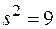 и выборочный центральный момент
и выборочный центральный момент 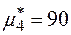 , найти доверительные интервалы для математического ожидания и дисперсии случайной величины Х, имеющей показательное распределение с плотностью вероятностей
, найти доверительные интервалы для математического ожидания и дисперсии случайной величины Х, имеющей показательное распределение с плотностью вероятностей 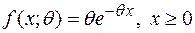 . Доверительную вероятность принять равной
. Доверительную вероятность принять равной 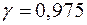 .
.
2.3.10. Показать, что в случае экспоненциального распределения с плотностью вероятностей 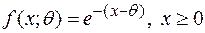 ,
, 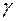 -доверительный интервал для
-доверительный интервал для 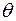 имеет вид:
имеет вид: 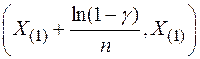 , где
, где 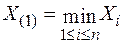 .
.
2.3.11. Пусть 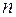 ,
, 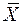 и
и 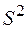 - соответственно объем, выборочное среднее и дисперсия выборки из генеральной совокупности, имеющей нормальное распределение с неизвестными параметрами. Показать, что с вероятностью
- соответственно объем, выборочное среднее и дисперсия выборки из генеральной совокупности, имеющей нормальное распределение с неизвестными параметрами. Показать, что с вероятностью 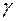 результат следующего,
результат следующего, 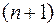 -го, наблюдения находится в интервале:
-го, наблюдения находится в интервале:
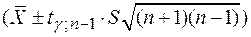 .
.
2.3.12. В результате пяти независимых взвешиваний одного и того же тела получены следующие результаты (в граммах): (4,12; 3,92; 4,55; 4,04; 4,35). Считая погрешности измерений нормальными 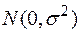 случайными величинами, указать доверительные границы для результатов предстоящего шестого взвешивания (доверительную вероятность принять равной
случайными величинами, указать доверительные границы для результатов предстоящего шестого взвешивания (доверительную вероятность принять равной 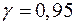 ).
).
 2015-04-01
2015-04-01 989
989








