Теорема. Пусть A 1, A 2,…, An – конечные множества и | A 1|= m 1, | A 2|= m 2,…, | An |= mn. Тогда | A 1´ A 2´…´ An |= m 1× m 2×…× mn.
Доказательство данной теоремы проведем методом математической индукции. Данный метод применим для доказательства утверждений A (n), имеющих смысл для натуральных чисел n и заключается в следующем:
1. Доказываем, что утверждение истинно для n =1, т.е. A (1) – истинно.
2. Предполагаем, что A (k) – истинно, k=2,3,…
3. Исходя из предположения A (k)– истинно доказываем истинность A (k +1). Из данного доказательства следует истинность утверждения A (n), для любого натурального числа n.
В нашем случае для n =1 истинность теоремы очевидна (| A 1|= m 1).
Предположим, что теорема верна для k =2,3,…, т.е. | A 1´…´ Ak |= m 1×…× mk.
Возьмем любой вектор (a 1,…, ak)Î A 1´…´ Ak и припишем ему справа элемент ak +1Î Ak +1. Поскольку | Ak +1|= mk +1, то это можно сделать mk +1 различными способами, т.е. получим mk +1, различных векторов из вектора (a 1,…, ak). Таким образом, из всех m 1×…× mk векторов, составляющих множество A 1´…´ Ak, приписыванием справа элемента ak +1Î Ak +1 можно получить m 1×…× mk × mk +1 векторов. Все полученные вектора различны и составляют множество A 1´…´ Ak ´ Ak +1. То есть | A 1´…´ Ak ´ Ak +1|= m 1×…× mk × mk +1 - теорема верна для k +1 и, следовательно, верна для любых натуральных n. Что и требовалось доказать.
Из доказанной теоремы следует 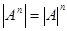 .
.
 2015-04-01
2015-04-01 1060
1060
