Способы уменьшения механических колебаний

При механических колебаниях, при наличии упругой связи скорость и момент изменяются по следующим законам:

; ;

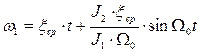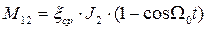- где 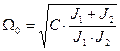– частота собственных колебаний;

С – приведённая жесткость упругого элемента();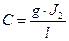

l – длина троса.

1) Из данных формул видно, что уменьшить колебания можно, если уменьшить ξ_ср, то есть, уменьшить М_пуск, т.о. двигатель должен иметь регулируемый М_пуск, т.е. увеличится t_пуск и понизится производительность.

2) Раскачивание груза можно предотвратить, если в момент времени 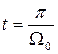со стороны двигателя приложить двойной М_пуск – обратного отклонения не происходит(М₁₂=М_дин) – дальнейшее движение груза происходит с двойным начальным ускорением.

Для реализации этого – двигатель с изменяемым М_пуск с D=2.

3) Уменьшить амплитуду колебаний можно путём формирования определённого закона управления во времени М_дин.

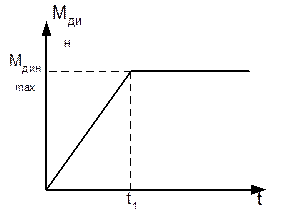
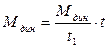(1)

Уравнения движения двухмассовой системы:

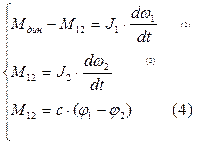
Разделим (2) на J₁,а (3) на J_2, продифференцируем (4) два раза:

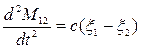(5), и подставим полученные (2) и (3):

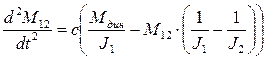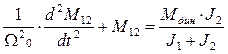(6) (7)

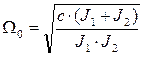- частота свободных колебаний.

Корни характеристического уравнения: p_1,2=±jΩ₀

тогда 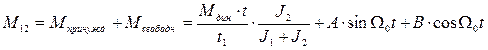(8)

Значения А и В находим из начальных условий:

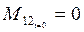(т.к. тело не может мгновенно изменить своё состояние), отсюда В=0

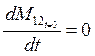, отсюда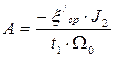

Таким образом уравнение изменения момента примет вид:

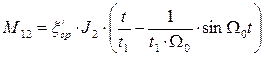(9)

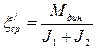
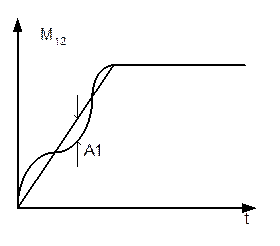А₁, А₂ – максимальное отклонение момента от среднего значения.

А₁ – постепенное изменение М_дин.

А₂ – скачкообразное изменение М_дин.

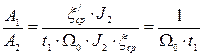
М_дин = М_{дин.макс} при ξ_ср =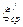

Чем больше время нарастания момента t₁, тем

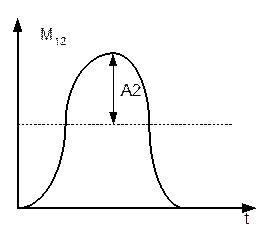меньше амплитуда колебаний.

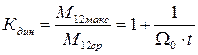
Ограничение темпа нарастания момента и первой производной благоприятно для переходных процессов: ρ=