2015-04-06
674
Пусть существует предел
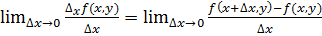. (2)
Тогда этот предел называется частной производной функции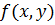 
в точке (х,у) и обозначается символом 
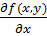. Коротко:
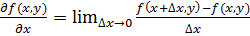. (3)
Аналогично определяется частная производная по y:
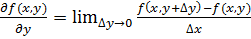. (4)
Ясно, что частная производная 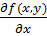- обычная производная функция 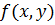по х при фиксированном аргументе у, а частная производна 
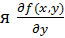- обычная производная по у при фиксированном аргументе х.
Ввиду этого, практическое нахождение частных производных сводится к обычному дифференцированию по какой-либо переменной при условии, что все остальные переменные фиксированные, т.е. постоянные.
До сих пор рассматривалось частные производные первого порядка. Поскольку они также являются функциями многих переменных, то можно еще раз найти частные производные. Получим частные производные второго порядка, которые обозначаются:
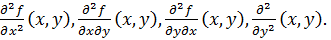(5)
Продолжая этот процесс, можно получить частные производные любого порядка.
Рассмотрим типовые задания с подробными решениями.
Пример 1. Вычислить частные производные функции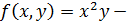 
|
|
|
.
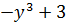Решение. Имеем: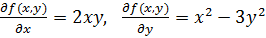 
.
Пример 2. Вычислить частные производные функции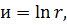 
где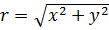 
по правилу дифференцирования сложной функции.
Решение.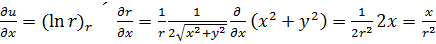 
Аналогично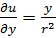 
Пример 3. Найти частные производные второго порядка от функции: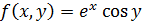 
.
Решение.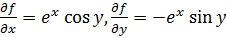 
Вычисляя от полученных выражений еще раз частные производные по x и по y, находим:
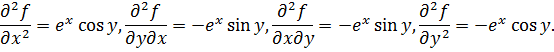
Обратим внимание на то, что смешанные производные второго порядка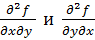 
тождественно равны, т.е. их значения оказались одинаковыми независимо от того, дифференцируем мы функцию f(x,y) сначала по x, а затем по у, или наоборот.
