Числовой ряд:
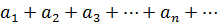 (21)
(21)
называется знакопеременным рядом, если среди его членов имеются как положительные, так и отрицательные числа. Числовой ряд называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки.
Признак Лейбница для знакочередующихся рядов.
Ряд сходится, если выполняются два условия: 1) его члены убывают по модулю; 2) общий член ряда стремится к нулю, т.е.
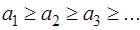 и
и 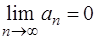 (22)
(22)
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд 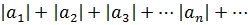 , составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
, составленный из абсолютных величин его членов, т.е. всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд сходится, а составленный из абсолютных величин его членов ряд расходится, то данный ряд называется условно сходящимся.
Рассмотрим типовые задания с подробными решениями.
Пример 1. Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд: 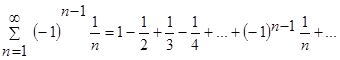
Решение: Члены данного ряда по абсолютной величине монотонно убывают: 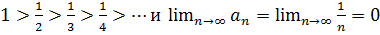 . Следовательно, согласно признаку Лейбница, ряд сходится. Ряд
. Следовательно, согласно признаку Лейбница, ряд сходится. Ряд 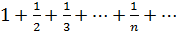 , составленный из абсолютных величин членов данного ряда, является гармоническим рядом, который, как известно, расходится. Поэтому данный ряд сходится условно.
, составленный из абсолютных величин членов данного ряда, является гармоническим рядом, который, как известно, расходится. Поэтому данный ряд сходится условно.
Пример 2. Исследовать сходимость знакопеременного ряда
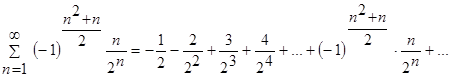
Решение: Составим ряд из абсолютных величин членов данного ряда: 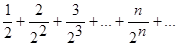 Для исследования этого ряда применим признак Даламбера. Имеем
Для исследования этого ряда применим признак Даламбера. Имеем 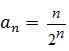 ,
, 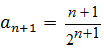 ,
, 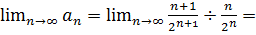
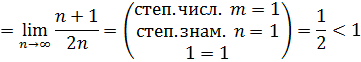
Ряд, составленный из абсолютных величин, сходится; следовательно, данный знакопеременный ряд сходится абсолютно.
 2015-04-06
2015-04-06 2921
2921








