2.1 Вычисление двойного интеграла в случае области 1 и 2го типа. Решение задач на приложения двойных интегралов
Определение двойного интеграла. Пусть в замкнутой ограниченной области D плоскости xОy определена непрерывная функция z = f (x,y). Разобьем области D производным образом на n частичных областей с площадями ∆S1, ∆S2,…, ∆Sn. В каждой i -й элементарной области ∆Si выберем производную точку Mi(xi,yi), умножим значение функции в этой точке f (xi,yi) на площадь ∆Si соответствующей области и составим сумму этих произведений, т.е.
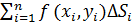 , (6)
, (6)
которая называется интегральной суммой функции 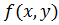 в области D. Двойным интегралом функции
в области D. Двойным интегралом функции 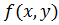 по области D называется предел этой суммы:
по области D называется предел этой суммы:
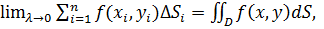 (7)
(7)
где 𝛌- наибольший из диаметров элементарных областей 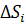 . Функция
. Функция 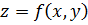 , для которой предел существует и конец, называется интегрируемой в этой области. В прямоугольных координатах дифференциал площади
, для которой предел существует и конец, называется интегрируемой в этой области. В прямоугольных координатах дифференциал площади 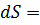
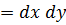 , тогда двойной интеграл примет вид:
, тогда двойной интеграл примет вид:
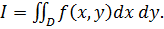 (8)
(8)
Если 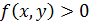 , то двойной интеграл функции
, то двойной интеграл функции 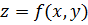 по области D равен объёму тела, ограниченного сверху поверхностью
по области D равен объёму тела, ограниченного сверху поверхностью 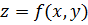 , сбоку цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит контур фигуры D, и снизу плоскостью z=0.
, сбоку цилиндрической поверхностью, образующие которой параллельны оси Oz, а направляющей служит контур фигуры D, и снизу плоскостью z=0.
Основные случаи вычисления двойного интеграла в прямоугольных координатах.
1) Если область D, в которой рассматривается двойной интеграл (8), есть прямоугольник со сторонами, параллельными координатным осям и заданными уравнениям 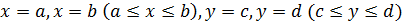 , то двойной интеграл вычисляется по одной из формул (9) или (10)
, то двойной интеграл вычисляется по одной из формул (9) или (10)
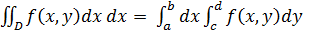 (9)
(9)
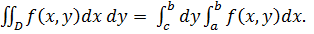 (10)
(10)
Интегралы в правых частях формул и называется повторными (или двукратными), а интегралы 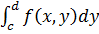 и
и 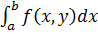 называются внутренними.
называются внутренними.
Под символом 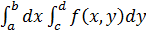 в формуле подразумевается дважды произведённое интегрирование. Первое интегрирование (внутреннее) по переменной y совершается в пределах от c до d в предположении, что x остаётся постоянным; результат интегрируется по переменной x в пределах от a до b.
в формуле подразумевается дважды произведённое интегрирование. Первое интегрирование (внутреннее) по переменной y совершается в пределах от c до d в предположении, что x остаётся постоянным; результат интегрируется по переменной x в пределах от a до b.
Если вычисление двойного интеграла выполняется по формуле, то порядок интегрирования меняется внутренний интеграл вычисляется по переменной x, причём y сохраняет постоянное значение, а внешние (повторное) интегрирование производится по переменной y. Графическое пояснение данного случая представлено на рисунке 2.
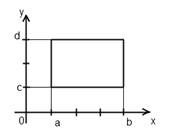
Рисунок 2 – Случай первый
2) Если область D такова, что любая прямая, проходящая внутри этой области и параллельная оси Oy, пересекает её границу в двух точках, то эта область называется простой относительной оси Ox и определяется системой неравенства вида: 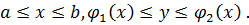 В этом случае двойной интеграл выражается через повторный интеграл по формуле:
В этом случае двойной интеграл выражается через повторный интеграл по формуле:
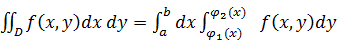 . (11)
. (11)
Графическое пояснение данного случая представлено на рисунке 3.
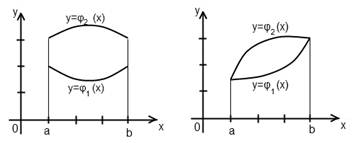
Рисунок 3 – Случай второй
3) Если граница области пересекается в двух точках всякой прямой, проходящей внутри этой области и параллельной оси Ox, то эта область называется простой относительно оси Oy и определяется системой неравенства вида: 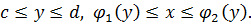
В этом случае двойной интеграл выражается формулой
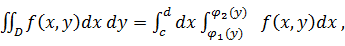 (12)
(12)
где интегрирование сначала выполняется по переменной x, а затем по переменной y.
Графическое пояснение данного случая представлено на рисунке 4.
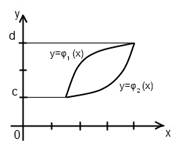
Рисунок 4 – Случай третий
4) Если нижняя или верхняя линии границы состоят из нескольких участков, имеющих различные уравнения, то область D, необходимо разбить прямыми, параллельными оси Oy, на такие части, чтобы каждый из участков выражался одним уравнением. В этом случае вычислении двойного интеграла сводится к вычислению двух (и более) повторных интегралов.
В случае, изображенном на рисунке 5, область D1 определяется системой неравенств 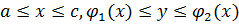 , а область D2 - системой неравенств
, а область D2 - системой неравенств 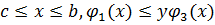 и, значит,
и, значит,
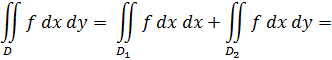
= 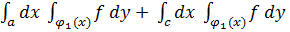 (13)
(13)
Графическое пояснение данного случая представлено на рисунке 5.
Рассмотрим типовые задания с подробными решениями.
Пример 1. Вычислить повторный интеграл 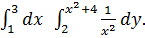
Решение. Согласно формуле 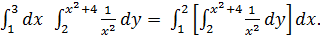
Вычислим сначала внутренний интеграл по переменной y, считая x постоянным:
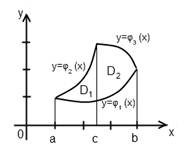
Рисунок 5 – Случай четвертый
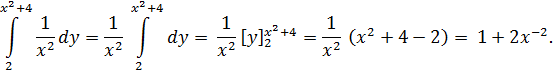
Теперь вычислим внешний интеграл по переменной x, подставив в него полученное выражение: 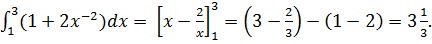
Пример 2. Вычислить двойной интеграл 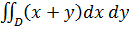 по области D, ограниченной прямыми x=2, x=6, y=1 y=4.
по области D, ограниченной прямыми x=2, x=6, y=1 y=4.
Решение. Область D, изображенная на рисунке 6, является простой относительно осей Ox и Oy, по этому для вычисления интеграла можно использовать любую из формул (9) или (10).
Сначала вычислим двойной интеграл по формуле:
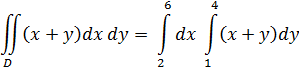
Вычислив внутренний интеграл по переменной y при постоянном x, находим:
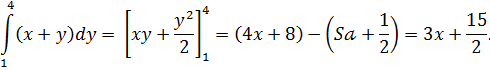
Подставив это выражение во внешний интеграл, получим
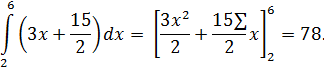
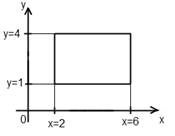
Рисунок 6 – Область D
Теперь вычислим двойной интеграл по формуле 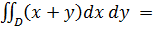
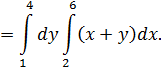
Найдём внутренний интеграл: 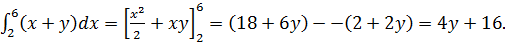
Далее найдём внешний интеграл: 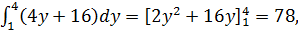 т.е. получим тот же ответ.
т.е. получим тот же ответ.
Пример 3. Вычислить двойной интеграл 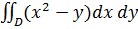 по области D, заданной системой неравенств
по области D, заданной системой неравенств 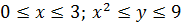 (рисунок 7). Решение. Область D является простой как относительно оси Ox, так и относительно оси Oy; поэтому вычислим этот интеграл двумя способами. Произведём сначала вычисления по формуле (11). Пределами внутреннего интеграла являются функции y=x2 и y=9, составляющие уравнения нижней и верхней границ области D, а пределами внешнего интеграла являются абсциссы x=0 и x=3. Значит,
(рисунок 7). Решение. Область D является простой как относительно оси Ox, так и относительно оси Oy; поэтому вычислим этот интеграл двумя способами. Произведём сначала вычисления по формуле (11). Пределами внутреннего интеграла являются функции y=x2 и y=9, составляющие уравнения нижней и верхней границ области D, а пределами внешнего интеграла являются абсциссы x=0 и x=3. Значит, 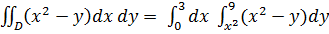
Вычислим внутренний интеграл по переменной y в предположении, что x - постоянная:
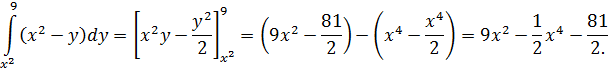
Вычислим внешний интеграл: 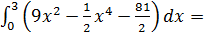
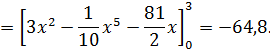
Произведём теперь вычисления по формуле (12). В этом случае область D выражается системой неравенств 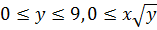 , т.е. приделами внутреннего интеграла служат функции x=0 и
, т.е. приделами внутреннего интеграла служат функции x=0 и 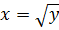 , а пределами внешнего интеграла – ординаты y=0 и y=9. Поэтому
, а пределами внешнего интеграла – ординаты y=0 и y=9. Поэтому 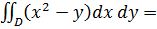
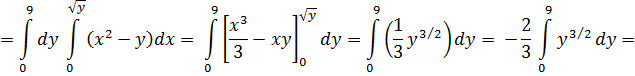
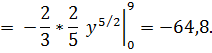
Пример 4. Вычислить двойной интеграл 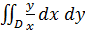 по области D, заданной линиями x=1, x=4, y=x и y=
по области D, заданной линиями x=1, x=4, y=x и y= 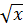 .
.
Решение. Находим точки пересечения этих линий:
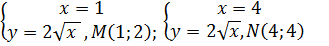
Область D, изображенная на рисунке 8, определяется системой неравенств 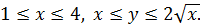
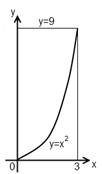
Рисунок 7 – Область D
Вычислим двойной интеграл по области D: 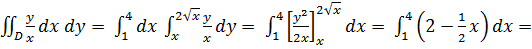
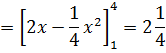
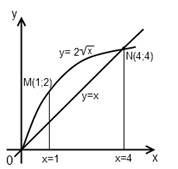
Рисунок 8 – Область D
Пример 5. Вычислить двойной интеграл 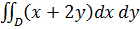 по области D, ограниченной линиями y=x, y=4x и y=
по области D, ограниченной линиями y=x, y=4x и y=  . Решение. Находим точки пересечения этих линий:
. Решение. Находим точки пересечения этих линий:
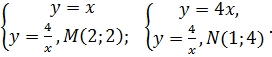
Область D, изображенная на рисунке 9, разобьем на две области D1 и D2, которые соответственно определяются системами неравенств 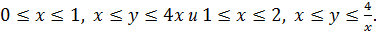
Вычислим двойной интеграл по области D1:
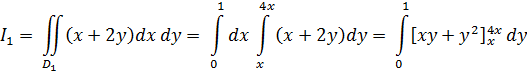
Вычислим двойной интеграл по области D2:
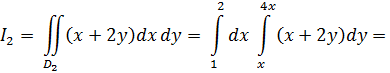
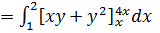 =
= 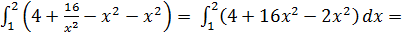
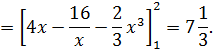
Значит, 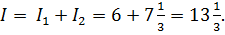
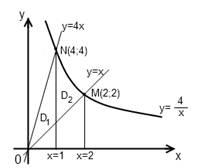
Рисунок 9 – Область D
Пример 6. Изменить порядок интегрирования в двойном интеграле 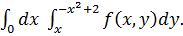 .
.
Решение. Зная пределы интегрирования, запишем область интегрирования D в виде системы неравенств 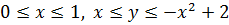 . Изобразим область на рисунке 10.
. Изобразим область на рисунке 10.
Построим линии x=0, x=1, y=x и y=1x2+2. Найдём точку пересечения линий 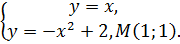
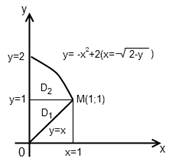
Рисунок 10 – Область D
Область D является простой относительно оси Ox. Рассмотрим область D относительно оси Oy. Через точку M(1;1), в которой стыкуются участки верхней границы области D, проведём прямую, параллельную оси Ox. Эта прямая делит область D на две области D1 и D2, которые запишем в виде систем неравенств:
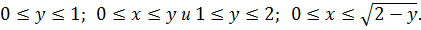
Тогда, получим:
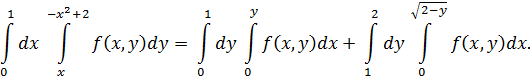
Объём цилиндрического тела, ограниченного сверху поверхностью 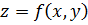 , снизу плоскостью z=0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z=0) область D, изображенную на рисунке 11, вычисляется по формуле
, снизу плоскостью z=0 и сбоку прямой цилиндрической поверхностью, вырезающей на плоскости xOy (z=0) область D, изображенную на рисунке 11, вычисляется по формуле
:
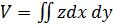 (14)
(14)
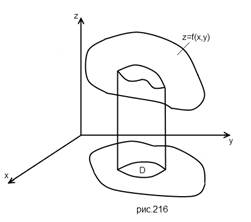
Рисунок 11 – Область D
Пример 7. Вычислить объём тела ограниченного поверхностями z=2x+1, x=0, y=4, y=x2.
Решение. Тело, ограниченное заданными поверхностями, представляет собой вертикальный параболический цилиндр, расположенный в I октанте. Сверху тело ограничено плоскостью z=2x+1, сбоку параболическим цилиндром y=x2 и плоскостями x=0 и y=4, снизу параболой y=x2 и прямыми x=0 и y=4. Найдём точки пересечения параболы y=x2 и прямой y=4:
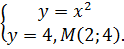 Значение x=-2 не рассматриваем, так как цилиндр расположен в I октанте.
Значение x=-2 не рассматриваем, так как цилиндр расположен в I октанте.
Область D запишем в виде системы неравенств 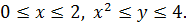
Получим 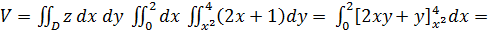
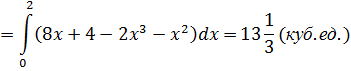
Пример 8. Вычислить объём тела, ограниченного поверхностями z=3-x-y, x2+y2=1 и z=0.
Решение. Данное тело есть прямой круговой цилиндр, ограниченный сверху плоскостью z=3-x-y, а снизу – кругом x2+y2=1 в плоскости z=0. Область D в основании цилиндра запишем в виде системы неравенств:
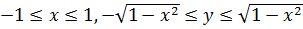 . Получим:
. Получим:
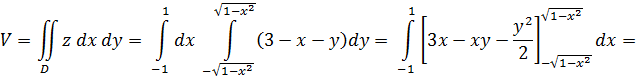
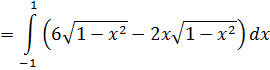
Первый интеграл вычисляется по формуле 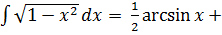
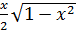 , второй - подстановкой 1-x2=z, -2xdx=dz; следовательно:
, второй - подстановкой 1-x2=z, -2xdx=dz; следовательно: 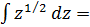
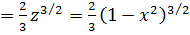 Окончательно находим объем:
Окончательно находим объем:
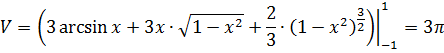
 2015-04-06
2015-04-06 5245
5245
