Исследование сходимости знакоположительных рядов

Числовым рядом называется выражение вида

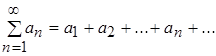, (15)

где 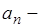общий член ряда.

Признаки сходимости числового (знакоположительного) ряда.

1) Необходимый признак

Ряд сходится, если

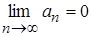, (16)

иначе ряд расходится.

2) Признак сравнения

Пусть даны два ряда с неотрицательными членами:

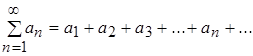(17)

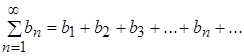(18)

Если 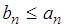для любого n, то из сходимости ряда (17) следует сходимость ряда (18); из расходимости ряда (18) следует расходимость ряда (17).

3) Признак Даламбера

Пусть дан ряд с положительными членами. Допустим, что существует

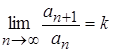. (19)

Тогда:

¾ если 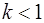, то ряд сходится;

¾ если 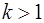, то ряд расходится;

¾ если 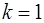, то о сходимости ничего сказать нельзя, (другой признак).

4) Признак Коши

Пусть дан ряд с положительными членами. Допустим, что существует

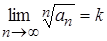. (20)

Тогда:

¾ если 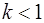, то ряд сходится

¾ если 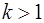, то ряд расходится

¾ если 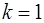, то о сходимости ничего сказать нельзя, (другой признак).

Вспомним алгоритм раскрытия неопределенности для вычисления пределов при .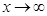

1) Найти m и n, где m – наивысшая степень числителя, n - наивысшая степень знаменателя;

2) Сравнить m и n:

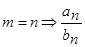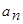¾ если , где и 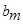коэффициенты пр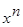и и ;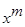

¾ если ;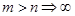

¾ если .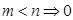

Рассмотрим типовые задания с подробными решениями.

Пример 1: Исследовать на сходимость .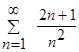

Решение: используем необходимый признак 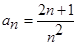. Подставим в формулу (16): 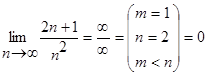. Ряд сходится.

Пример 2: Исследовать на сходимость .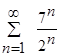

Решение: используем признак Коши. 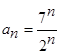. Подставим в формулу (20): 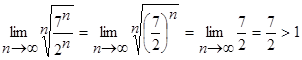. Ряд расходится.

Пример 3: Исследовать на сходимость .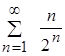

Решение: используем признак Даламбера. 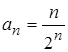, тогда

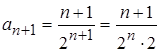. Подставим в формулу (19):

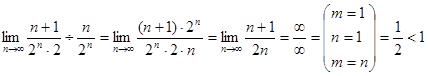. Ряд сходится.

Пример 4: Исследовать на сходимость ряд .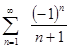

Решение: 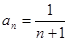. По признаку Лейбница ряд расходится, т.к.: Первое условие 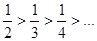- выполняется. Второе условие 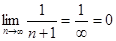- выполняется